SOLVING EQUATIONS HARDER QUESTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
If
(x/b) + (b/x) = (a/b) + (b/a)
the roots of the equation are
Solution :
(x/b) + (b/x) = (a/b) + (b/a)
(x2+b2)/bx = (a2+b2)/ab
ab (x2+b2) = bx (a2+b2)
abx2+ab3 = a2b x + b3x
abx2+ab3-a2bx-b3x = 0
abx2+(-a2b-b3)x+ab3 = 0
a = ab, b = (-a2b- b3), c = a b3
x = [-b±√(b2-4ac)]/2a ----(1)
b2-4ac = (-a2b- b3)2 - 4(ab)(ab3)
= (a2b+ b3)2 - 4(ab)(ab3)
= a4b2+2a2b4+b6 - 4a2b4
= a4b2-2a2b4+b6
= (a2b- b3)2
√(b2-4ac) = (a2b- b3)
By applying the value of √(b2-4ac) in (1), we get
x = [-(-a2b- b3) ± (a2b- b3)]/2(ab)
x = [-(-a2b-b3)+(a2b- b3)]/2ab
(or)
x = [-(-a2b- b3) - (a2b- b3)]/2(ab)
x = (a2b+b3+a2b-b3)/2ab
x = (a2b+b3+a2b-b3)/2ab
x = 2a2b/2ab
x = a
x = [-(-a2b- b3) - (a2b- b3)]/2(ab)
x = (a2b+b3-a2b+b3)/2ab
x = 2b3/2ab
x = b2/a
So, the solution is {a, b2/a}.
Question 2 :
The values of x in the equation
7(x+2p)2+5p2 = 35xp+117 p2
Solution :
7(x+2p)2+5p2 = 35xp+117p2
7(x2+4xp+4p2)+5p2 = 35xp+117p2
7x2+28xp+28p2+5p2 = 35xp+117p2
7x2+28xp-35xp+28p2-117p2+5p2 = 0
7x2-7xp-84p2 = 0
x2-xp-12p2 = 0
x2-4xp+3xp-12p2 = 0
x(x-4p)+3p(x-4p) = 0
(x+3p)(x-4p) = 0
By solving, we get
x = -3p and x = 4p
So, the solution is {-3p, 4p}.
Question 3 :
Solving equation
(b-c) x2 + (c-a) x + (a-b) = 0
Solution :
a = b-c, b = c-a, c = a-b
x = [-b±√(b2-4ac)]/2a ------(1)
b2-4ac = (c-a)2-4(b-c)(a-b)
= c2+a2-2ac-4(ab-b2-ac+bc)
= c2+a2-2ac-4ab+4b2+4ac-4bc
= c2+a2+2ac-4ab+4b2-4bc
= a2+4b2+c2-4ab-4bc+2ac
= (a-2b+c)2
√(b2-4ac) = a-2b+c
By applying the value of √(b2-4ac) in (1), we get
x = [-(c-a) ± (a-2b+c)]/2(b-c)
x = [-(c-a)+(a-2b+c)]/2(b-c)
(or)
x = [-(c-a)-(a-2b+c)]/2(b-c)
x = [-(c-a)+(a-2b+c)]/2(b-c)
x = (-c+a+a-2b+c)/2(b-c)
x = 2(a-b)/2(b-c)
x = (a-b)/(b-c)
x = [-(c-a)-(a-2b+c)]/2(b-c)
x = (-c+a-a+2b-c)/2(b-c)
x = 2(b-c)/2(b-c)
x = 1
So, the solution is { (a-b)/(b-c), 1 }.
Question 4 :
The values of x satisfying the equation
√(2x2+5x-2)-√(2x2+5x-9) = 1
Solution :
√(2x2+5x-2)-√(2x2+5x-9) = 1
Taking squares on both sides, we get
(√(2x2+5x-2)-√(2x2+5x-9))2 = 12
(2x2+5x-2)+(2x2+5x-9)-2√(2x2+5x-2)√(2x2+5x-9) = 1
4x2+10x-11-2√(2x2+5x-2)√(2x2+5x-9) = 1
4x2+10x-12 = 2√(2x²+5x-2)(2x²+5x-9)
2x2+5x-6 = √(2x²+5x-2)(2x²+5x-9)
(2x2+5x-6)2 = (2x²+5x-2)(2x²+5x-9)
(2x2)2+(5x)2+(-6)2+2(2x2)(5x)+2(5x)(-6)+2(-6)(2x2)
= 4x4+10x3-18x2+10x3+25x2-45x-4x2-10x+18
4x4+25x2+36+20x3-60x-24x2 =
4x4+20x3-22x2+25x2-45x-10x+18
4x4+25x2+36+20x3-60x-24x2 = 4x4+20x3+3x2-55x+18
4x4-4x4+20x3-20x3+x2-3x2-60x+55x+36-18 = 0
-2x2-5x+18 = 0
2x2+5x-18 = 0
(2x+9) (x-2) = 0
By solving, we get
x = -9/2 and x = 2
So, the solution is {-9/2, 2}.
Question 5 :
The values of x satisfying the equation
Solving equation
6 (√[x/(1-x)]+√[(1-x)/x]] = 15
Solution :
[√x/√(1 - x)] + [√(1 - x)/√x] = 15/6
By taking least common multiple,
(√x√x)+[√(1-x)√(1-x)]/√x(1-x) = 5/2
x+(1-x)/√(x - x2) = 5/2
2 = 5√(x - x2)
Taking squares on both sides
22 = (5√(x-x2))2
4 = 25 (x-x2)
4 = 25x-25x2
25x2-25x+4 = 0
25x2-20x-5x+4 = 0
(5x-1) (5x-4) = 0
x = 1/5 and x = 4/5
Solution is {1/5, 4/5}.
Question 6 :
Solving equation
z2-6z+9 = 4√(z2-6z+6)
following roots are obtained
Solution :
z2-6z+9 = 4√(z2-6z+6)
To remove square root on right side we have to take squares on both sides.
(z2-6z+9)2 = [4√(z2-6z+6)]²
(z2- 6 z + 9)2 = (z2)2+(6z)2+92-2z2(6z) - 2(6z)(9) + 2(9) (z2)
= z4+36z2+81-12z3-108z+18z2
(z2-6z+9)2 = [4√(z2-6z+6)]2
[z4+36z2+81-12z3-108z+18z2] = 16(z2-6z+6)
[z4+36z2+81-12z3-108z+18z2] = 16z2-96z+96
z4-12z3+38z2-12z-15 = 0
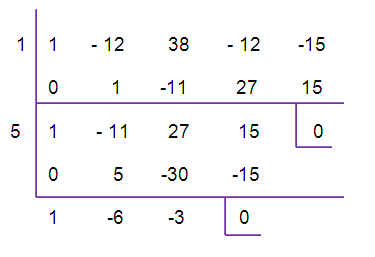
By solving the remaining quadratic equation, we can find other two roots
z2-6z-3 = 0
z = [- b ± √(b2-4ac)]/2a
a = 1, b = -6 and c = -3
z = [-(-6) ± √(-6)²-4(1)(-3))]/2(1)
z = (6±√48)/2
z = (6±4√3]/2
z = 3+2√3 and z = 3-2√3
Solution is { 1, 5, 3+2√3, 3-2√3 }.
Question 7 :
When
√(2z+1) + √(3z+4) = 7
the value of z is given by
Solution :
√(2z+1)+√(3z+4) = 7
By taking squares on both sides, we get
[√(2z+1)+√(3z+4)]2 = 72
[√(2z+1)]2 + [√(3z+4)]2 + 2√(2z+1) (3z+4) = 49
2z+1+3z+4+2√(6z2+11z+4) = 49
5z+5+2√(6z2+11z+4) = 49
2√(6z2+11z+4) = 49-5z-5
2√(6z2+11z+4) = 44-5z
By taking squares on both sides, we get
[2√(6z2+11z+4)w]2 = (44-5z)2
4 (6z2+11z+4) = 442-2(44) (5z)+(5z)²
24z2+44z+16 = 1936-440z+25z2
25z2-24z2-440z-44z+1936-16 = 0
z2-484z+1920 = 0
z2-480z-4z+1920 = 0
(z-4) (z-480) = 0
z = 4 and z = 480
solution are x = 4 and x = 480.
Question 8 :
log4(x2 + x) - log4(x + 1) = 2. Find x.
Solution :
L.H.S:
log4(x2 + x) - log4(x + 1) = 2
Using the property of logarithm,
log m - log n = log (m/n)
log4[(x2 + x)/(x + 1)] = 2
[(x2 + x)/(x + 1)] = 42
Factoring x from the numerator, we get
x(x + 1) / (x + 1) = 16
x = 16
So, the value of x is 16.
Question 9 :
[log10(√ 25) - log10 (2)3 + log1042]x
Solution :
= [log10(√ 25) - log10(2)3 + log1042]x
= [log10(√(5 x 5)) - log108 + log1016]x
= [log10(5) - log108 + log1016]x
= [log10(5) + log1016 - log108]x
= [log10(5x16)/8]x