SOLVING EQUATIONS WITH FRACTIONS

Example 1-9 : Solve for x.

Example 1 :

ˣ⁄₅ = 2

Solution :

ˣ⁄₅ = 2

In the equation above, there is only one denominator 5.

Multiply both sides of the equation by 5 to get rid of the denominator 5.

5(ˣ⁄₅) = 5(2)

x = 10

Example 2 :

³ˣ⁄₂ = 4.5

Solution :

³ˣ⁄₂ = 4.5

In the equation above, there is only one denominator 2.

Multiply both sides of the equation by 2 to get rid of the denominator 2.

2(³ˣ⁄₂) = 2(4.5)

3x = 9

Divide both sides of the equation by 3.

x = 3

Example 3 :

ˣ⁄₆ = ⁵⁄₉

Solution :

ˣ⁄₆ = ⁵⁄₉

In the equation above, there are two deominators 6 and 9.

Least common multiple of (6, 9) = 18.

Multiply both sides of the equation by 18 to get rid of the denominators .

18(ˣ⁄₆) = 18(⁵⁄₉)

3x = 2(5)

3x = 10

Divide both sides of the equation by 3.

x = ¹⁰⁄₃

Example 4 :

ˣ⁄₄ + 3 = ˣ⁄₆ + 7

Solution :

ˣ⁄₄ + 3 = ˣ⁄₆ + 7

In the equation above, there are two denominators 4 and 6.

Least common multiple of (4, 6) = 12.

Multiply both sides of the equation by 12 to get rid of the denominators 4 and 6.

12(ˣ⁄₄ + 3) = 12(ˣ⁄₆ + 7)

12(ˣ⁄₄) + 12(3) = 12(ˣ⁄₆) + 12(7)

3x + 36 = 2x + 84

Subtract 2x from both sides.

x + 36 = 84

Subtract 84 from both sides.

x = 48

Example 5 :

⁷ˣ⁄₁₀ + ³⁄₂ = ³ˣ⁄₅ + 2

Solution :

In the equation above, there are three denominators 10, 2 and 5.

Find the least common multiple of 10, 2 and 5 uising division method.

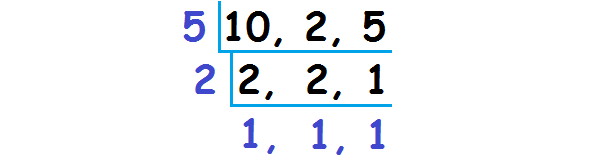
Least common multiple of (10, 2, 5) :

= 5 ⋅ 2 ⋅ 1 ⋅ 1 ⋅ 1

= 10

Multiply both sides of the equation by 10 to get rid of the denominators 10, 2 and 5. 

10(⁷ˣ⁄₁₀ + ³⁄₂) = 10(³ˣ⁄₅ + 2)

Using Distributive Property.

10(⁷ˣ⁄₁₀) + 10(³⁄₂) = 10(³ˣ⁄₅) + 10(2)

7x + 5(3) = 2(3x) + 20

7x + 15 = 6x + 20

Subtract 6x from both sides.

x + 15 = 20

Subtract 15 from both sides.

x = 5

Example 6 :

ˣ⁄₇ - 6 = ³ˣ⁄₇ + 4

Solution :

ˣ⁄₇ - 6 = ³ˣ⁄₇ + 4

In the equation above, there is only one denominator, that is 7.

Multiply both sides of the equation by 7 to get rid of the denominator 7.

7(ˣ⁄₇ - 6) = 7(³ˣ⁄₇ + 4)

7(ˣ⁄₇) + 7(-6) = 7(³ˣ⁄₇) + 7(4)

x - 42 = 3x + 28

Subtract x from both sides.

-42 = 2x + 28

Subtract 28 from both sides.

-70 = 2x

Divide both sides by 2.

-35 = x

Example 7 :

⁴ˣ⁄₅ - ⁷⁄₄ = ˣ⁄₅ + ˣ⁄₄

Solution :

⁴ˣ⁄₅ - ⁷⁄₄ = ˣ⁄₅ + ˣ⁄₄

In the equation above, there are two different denominators 5 and 4.

Least common multiple of (5, 4) = 20.

Multiply both sides of the equation by 20 to get rid of the denominators 5 and 4.

20(⁴ˣ⁄₅ - ⁷⁄₄) = 20(ˣ⁄₅ + ˣ⁄₄)

Using Distributive Property. 

20(⁴ˣ⁄₅) - 20(⁷⁄₄) = 20(ˣ⁄₅) + 20(ˣ⁄₄)

4(4x) - 5(7) = 4(x) + 5(x)

16x - 35 = 4x + 5x

16x - 35 = 9x

Subtract 9x from both sides.

7x - 35 = 0

Add 35 to both sides.

7x = 35

Divide both sides by 7.

x = 5

Example 8 :

⁽²ˣ ⁻ ³⁾⁄₂ = ⁽⁻ˣ ⁻ ¹⁾⁄₄

Solution :

⁽²ˣ ⁻ ³⁾⁄₂ = ⁽⁻ˣ ⁻ ¹⁾⁄₄

In the equation above, there is only one fraction on each side. So, the equation can be solved by cross multiplication.

That is, numerator on the left side has to be multiplied by denominator on the right side and numerator on the right side has to be multiplied by denominator on the left side.

4(2x - 3) = 2(-x - 1)

Using Distributive Property,

8x - 12 = -2x - 2

Add 2x to both sides.

10x - 12 = -2

Add 12 to both sides.

10x = 10

Divide both sides by 10.

x = 1

Example 9 :

⁽⁴ˣ ⁺ ⁵⁾⁄₃ - ³ˣ⁄₂ = -x

Solution :

⁽⁴ˣ ⁺ ⁵⁾⁄₃ - ³ˣ⁄₂ = -x

In the equation above, there are two denominators 3 and 2.

Least common multiple of (3, 2) = 6.

Multiply both sides of the equation by 6 to get rid of the denominators 3 and 2.

6(⁽⁴ˣ ⁺ ⁵⁾⁄₃ - ³ˣ⁄₂) = 6(-x)

Using Distributive Property. 

6(⁽⁴ˣ ⁺ ⁵⁾⁄₃) - 6(³ˣ⁄₂) = -6x

2(4x + 5) - 3(3x) = -6x

8x + 10 - 9x = -6x

-x + 10 = -6x

Add 6x to both sides.

5x + 10 = 0

Subtract 10 from both sides.

5x = -10

Divide both sides by 5.

x = -2

Example 10 :

Two times the reciprocal of a number and 3 add up to ¹⁷⁄₅. What is the number?

Solution :

Let x be the number.

It is given that the sum two times the reciprocal of the number and 3 is equal to ¹⁷⁄₅.

2(¹⁄ₓ) + 3 = ¹⁷⁄₅

²⁄ₓ + 3 = ¹⁷⁄₅

Multiply both sides of the equation by 5x to get rid of the denominators x and 5.

5x(²⁄ₓ + 3) = 5x(¹⁷⁄₅)

5x(²⁄ₓ) + 5x(3) = 17x

10 + 15x = 17x

Subtract 15x from both sides.

10 = 2x

Divide both sides by 2.

5 = x

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.