SOLVING EQUATIONS AND INEQUALITIES BY GRAPHING WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Solve the following equation by graphing :
-3x + 20 = 5
Problem 2 :
Solve the following equation by graphing :
|x - 4| = 0.5x + 1
Problem 3 :
Solve the following inequality by graphing :
-3x + 20 > 5
Problem 4 :
Solve the following equation by graphing :
x2 - 4 > 0

Answers
1. Answer :
An equation is a statement that two expressions are equal. The values of x that make the equation true are the solutions.
To have an equation by graphing, write two new equations by setting y equal to each in the original equation.
-3x + 20 = 5
y = -3x + 20 y = 5
Graph the two equations and identify the points of intersection. These points will have x-values that produce the same y-values for both expressions.
Each of the x-values is a solution to the original equation.
Graph y = -3x + 20 and y = 5.
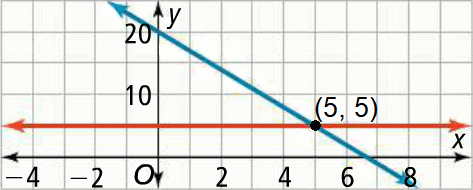
It appears that y = -3x + 20 and y = 5 intersect at
x = 5
By substituting this value into the original equation, we can verify the result.
That is,
-3(5) + 20 = 5
-15 + 20 = 5
5 = 5
This is the only point on the graph where the value of the functions y = -3x + 20 and y = 5 are equal.
So, the solution to the equation -3x + 20 = 5 is
x = 5
2. Answer :
|x - 4| = 0.5x + 1
As we have done in the above problem, write two new equations by setting y equal to each in the original equation.
|x - 4| = 0.5x + 1
y = |x - 4| y = 0.5x + 1
Graph the two equations and identify the points of intersection. These points will have x-values that produce the same y-values for both expressions.
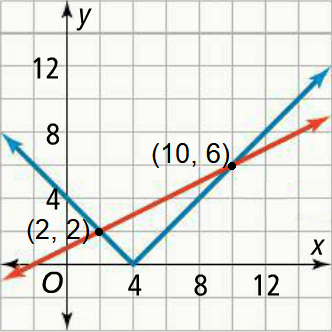
It appears that y = |x - 4| and y = 0.5x + 1 intersect at
x = 2 and x = 10
By substituting these values into the original equation, we can verify the result.
That is,
|
When x = 2, |2 - 4| = 0.5(2) + 1 |-2| = 1 + 1 2 = 2 |
When x = 10, |10 - 4| = 0.5(10) + 1 |6| = 5 + 1 6 = 6 |
So, the solutions to the equation |x - 4| = 0.5x + 1 are
x = 2 and x = 10
3. Answer :
-3x + 20 > 5
To solve the inequality, we have to identify the values of x that make the value of the expression -3x + 20 greater than 5.
To have an inequality by graphing, write two new equations by setting y equal to each in the original inequality.
-3x + 20 > 5
y = -3x + 20 y = 5
Graph the two equations and identify the points of intersection. These points will have x-values that produce the same y-values for both expressions.
Graph y = -3x + 20 and y = 5.
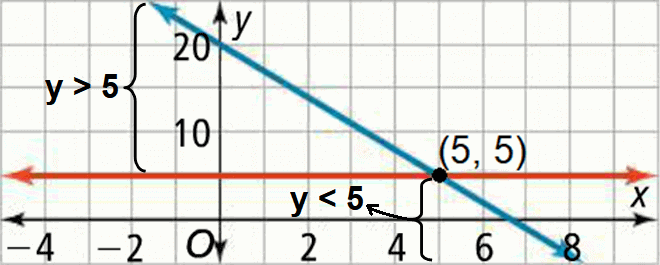
From the point of intersection, it is clear that y = 5 when x = 5.
In the above graph, y > 5 when x < 5.
That is,
-3x + 20 > 5 when x < 5
So, the solution to the inequality -3x + 20 > 5 is
x < 5 or x ∈ (-∞, 5)
4. Answer :
x2 - 4 > 0
To solve the inequality, we have to identify the values of x that make the value of the expression x2 - 4 greater than 0.
Graph the equation y = x2 - 4 by translating the parent function y = x2 down 4 units.
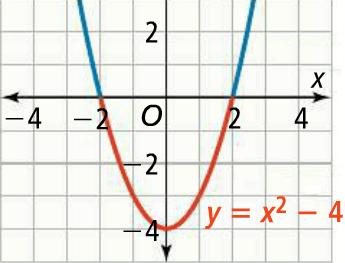
In the above graph, y > 0 when
x < -2 and x > 2
That is, x2 - 4 > 0 when
x < -2 and x > 2
So, the solution to the inequality x2 - 4 > 0 is
x < -2 or x > 2
or
x ∈ (-∞, 2)U(2, ∞)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact US | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation

