SOLVING CUBIC EQUATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Every cubic equation would have 3 solutions. To solve a cubic equation, either the method factoring or synthetic division can be used.
If a cubic equation equation is factorable, factor it by grouping and solve for the variable.
Synthetic division can be used for the cubic equations which can not be factored by grouping.
Solve each of the following cubic equations.
Question 1 :
x3 + 2x2 - x - 2 = 0
Solution :
The given cubic equation can be factored by grouping.
Factor and solve.
x3 + 2x2 - x - 2 = 0
x2(x + 2) - 1(x + 2) = 0
(x + 2)(x2 - 1) = 0
|
x + 2 = 0 x = -2 |
x2 - 1 = 0 x2 - 12 = 0 (x + 1)(x - 1) = 0 x = -1 or x = 1 |
So, the solution is {-2, -1, 1}.
Question 2 :
2x3 - x2 - 4x + 2 = 0
Solution :
The given cubic equation can be factored by grouping.
Factor and solve.
2x3 - x2 - 4x + 2 = 0
x2(2x - 1) - 2(2x - 1) = 0
(2x - 1)(x2 - 2) = 0
|
2x - 1 = 0 x = 1/2 |
x2 - 2 = 0 x2 = 2 x = ±√2 |
So, the solution is {1/2, √2, -√2}.
Question 3 :
x3 - 2x2 - 5x + 6 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
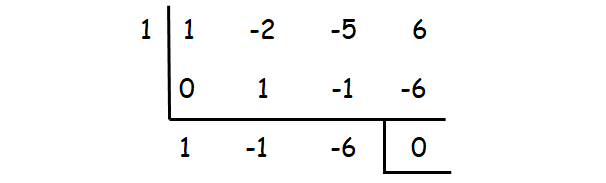
1 is one of the roots. The other roots can be determined by solving the quadratic equation
x2 - x - 6 = 0
Factor and solve.
(x - 3)(x + 2) = 0
x = 3 or x = -2
So, the solution is {1, 3, -2}.
Question 4 :
4x3 - 7x + 3 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
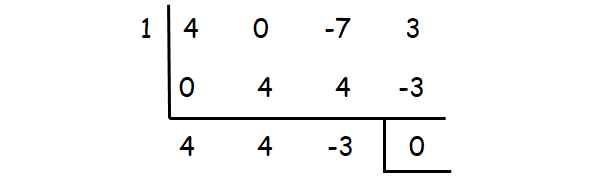
1 is one of the roots. The other roots can be determined by solving the quadratic equation
4x2 + 4x - 3 = 0
Factor and solve.
4x2 + 6x - 2x - 3 = 0
2x(2x + 3) - 1(2x + 3) = 0
(2x + 3)(2x - 1) = 0
x = -3/2 or x = 1/2
So, the solution is {1, -3/2, 1/2}.
Question 5 :
x3 - 23x2 + 142x - 120 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
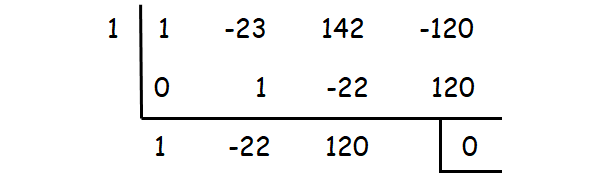
1 is one of the roots. The other roots can be determined by solving the quadratic equation
x2 - 22x + 120 = 0
Factor and solve.
(x - 10)(x - 12) = 0
x = 10 or x = 12
So, the solution is {1, 10, 12}.
Question 6 :
4x3 - 5x2 + 7x - 6 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
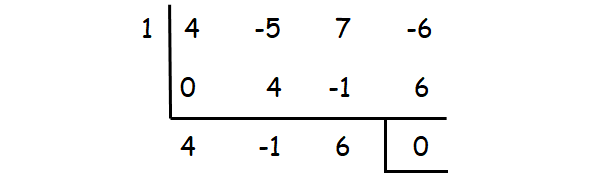
1 is one of the roots. The other roots can be determined by solving the quadratic equation
4x2 - x + 6 = 0
This quadratic equation can not be solved by factoring. So use quadratic formula and solve.
x = [-b ± √(b2 - 4ac)]/2a
a = 4, b = -1 and c = 6,
x = (1 ± √-95)/8
For the given cubic equation, there is only one real root, that is 1. The remaining two roots are imaginary.
Question 7 :
x3 - 7x + 6 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
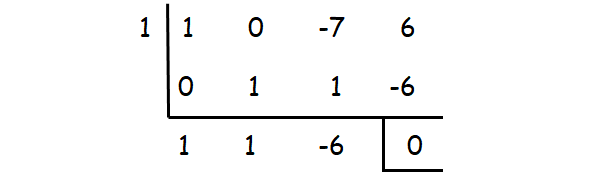
1 is one of the roots. The other roots can be determined by solving the quadratic equation
x2 + x - 6 = 0
Factor and solve.
(x + 3)(x - 2) = 0
x = -3 or x = 2
So, the solution is {1, -3, 2}.
Question 8 :
x3 + 13x2 + 32x + 20 = 0
Solution :
Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.
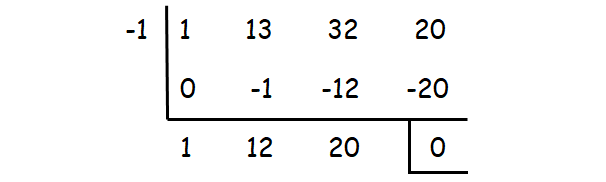
-1 is one of the roots. The other roots can be determined by solving the quadratic equation
x2 + 12x + 20 = 0
Factor and solve.
(x + 2)(x + 10) = 0
x = -2 or x = -10
So, the solution is {-1, -2, -10}.
Question 9 :
Find the remainder of
f(x) = x3 + x2 - 6x - 7
divided by x + 2
Solution :
x + 2 = 0
x = -2
f(-2) = (-2)3 + (-2)2 - 6(-2) - 7
= -8 + 4 + 12 - 7
= -15 + 16
= 1
While dividing the polynomial by x + 2, we get the remainder 1.
Question 10 :
Find the value of k if
f(x) = 3(x2 + 3x - 4) - 8(x - k) is divisible by x.
Solution :
Since it is divsible by x, the x = 0
f(0) = 3(02 + 3(0) - 4) - 8(0 - k)
Since it is divisible by x, the remainder will be 0.
0 = 3(0 + 0 - 4) - 8(-k)
0 = -12 + 8k
8k = 12
k = 12/8
k = 3/2
So, the value of k is 3/2.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41) -
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems


