SOLVING CUBIC EQUATIONS WORKSHEET

Solve each of the following cubic equations.

1) x³ + 2x² - x - 2 = 0

2) 2x³ - x² - 4x + 2 = 0

3) x³ - 2x² - 5x + 6 = 0

4) 4x³ - 7x + 3 = 0

5) x³ - 23x² + 142x - 120 = 0

6) 4x³ - 5x² + 7x - 6 = 0

7) x³ - 7x + 6 = 0

8)  x³ + 13x² + 32x + 20 = 0

9)   The graph of 

f(x) = ax³ + x² - 18x - 9

intersects the -x axis at (3,0). What is the value of a?

A) -1     B) 0     C) 1     D) 2

10)  In the -xy plane, the graph of function f has -x intercepts at -7,  -5 and 5. Which of the following could define f ? 

A) (x - 7)(x² - 25)        B) (x - 7)(x² + 25)

C) (x + 7)(x² - 25)        D) (x + 7)(x² + 25)

1. Answer :

x³ + 2x² - x - 2 = 0

The given cubic equation can be factored by grouping.

Factor and solve.

x³ + 2x² - x - 2 = 0

x²(x + 2) - 1(x + 2) = 0

(x + 2)(x² - 1) = 0

So, the solution is {-2, -1, 1}.

2. Answer :

2x³ - x² - 4x + 2 = 0

The given cubic equation can be factored by grouping.

Factor and solve.

2x³ - x² - 4x + 2 = 0

x²(2x - 1) - 2(2x - 1) = 0

(2x - 1)(x² - 2) = 0

So, the solution is {1/2, √2, -√2}.

3. Answer :

x³ - 2x² - 5x + 6 = 0

Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division. 

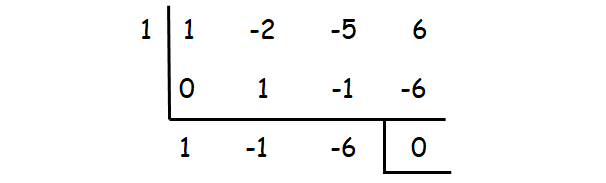
1 is one of the roots. The other roots can be determined by solving the quadratic equation

x² - x - 6 = 0

Factor and solve.

(x - 3)(x + 2) = 0

x = 3 or x = -2

So, the solution is {1, 3, -2}.

4. Answer :

4x³ - 7x + 3 = 0

Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division. 

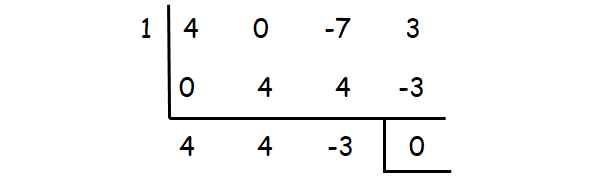
1 is one of the roots. The other roots can be determined by solving the quadratic equation

4x² + 4x - 3 = 0

Factor and solve.

4x² + 6x - 2x - 3 = 0

2x(2x + 3) - 1(2x + 3) = 0

(2x + 3)(2x - 1) = 0

x = -3/2 or x = 1/2

So, the solution is {1, -3/2, 1/2}.

5. Answer :

x³ - 23x² + 142x - 120 = 0

Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.

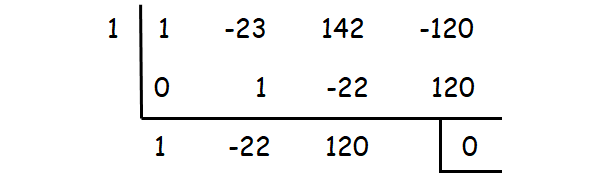
1 is one of the roots. The other roots can be determined by solving the quadratic equation

x² - 22x + 120 = 0

Factor and solve.

(x  - 10)(x - 12) = 0

x = 10 or x = 12

So, the solution is {1, 10, 12}.

6. Answer :

4x³ - 5x² + 7x - 6 = 0

Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.

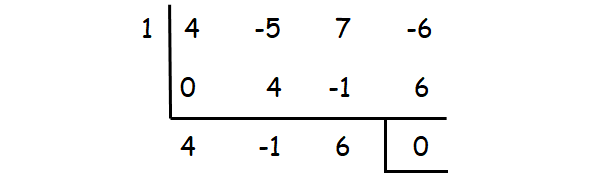
1 is one of the roots. The other roots can be determined by solving the quadratic equation

4x² - x + 6 = 0

This quadratic equation can not be solved by factoring. So use quadratic formula and solve.

x = [-b ± √(b² - 4ac)]/2a

a = 4, b = -1 and c = 6,

x = (1 ± √-95)/8

For the given cubic equation, there is only one real root, that is 1. The remaining two roots are imaginary. 

7. Answer :

x³ - 7x + 6 = 0

Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.

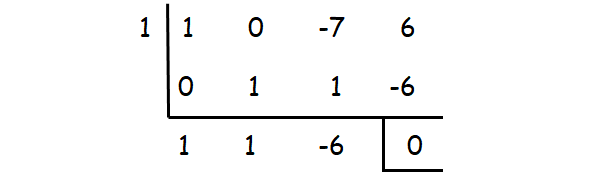
1 is one of the roots. The other roots can be determined by solving the quadratic equation

x² + x - 6 = 0

Factor and solve.

(x + 3)(x - 2) = 0

x = -3 or x = 2

So, the solution is {1, -3, 2}.

8. Answer :

 x³ + 13x² + 32x + 20 = 0

Check whether the values 1, -1, 2, -2, ...... could be one of the solutions using synthetic division.

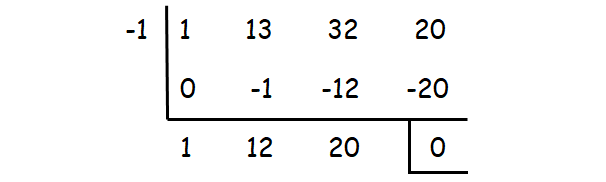
-1 is one of the roots. The other roots can be determined by solving the quadratic equation

x² + 12x + 20 = 0

Factor and solve.

(x + 2)(x + 10) = 0

x = -2 or x = -10

So, the solution is {-1, -2, -10}.

9. Answer : 

f(x) = ax³ + x² - 18x - 9

Since the graph intersects at (3, 0)

f(3) = a(3)³ + 3² - 18(3) - 9

0 = 27a + 9 - 54 - 9

0 = 27a - 54

27a = 54

a = 54/27

a = 2

So, the value of a is 2.

10. Answer :

The roots are x = -7, x = -5 and x = 5

The factors are (x + 7)(x + 5)(x - 5)

= (x + 7)(x² - 5²)

= (x + 7)(x² - 25)

So, option C is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.