SOLVING CUBIC EQUATIONS WHEN ADDITIONAL INFORMATION OF ROOTS ARE GIVEN

Question 1 :

Solve the equation 3x³ − 26x² + 52x − 24 = 0 if its roots form a geometric progression.

Solution :

Let the roots of the cubic equation be a/r, a and ar.

By comparing the given equation with general form of cubic equation, we get 

a = 3, b = -26, c = 52 and d = -24.

In any cubic equation ,

Sum of roots  =  -b/a  =  26/3

Product of roots  =  -d/a  =  24/3  =  8

(a/r) + a + ar  =  26/3 

a[(1 + r + r²)/r]  =  26/3  ---(1)

(a/r) a (ar)  =  8

a³  =  8, a = 2

By applying the value of a in (1), we get

2[(1 + r + r²)/r]  =  26/3

[(1 + r + r²)/r]  =  13/3

3r² + 3r + 3  =  13r

3r² - 10r + 3  =  0

r = 1/3, r = 3

When a = 2 and r = 3

a/r = 2/3, a = 2 and ar  =  2(3) = 6

Hence the roots are 2/3, 2 and 6.

Question 2 :

Determine k and solve the equation 2x³ − 6x² + 3x + k = 0 if one of its roots is twice the sum of the other two  roots.

Solution :

Let a, b and c be the roots of the cubic equation.

a = 2(b + c)

Sum of roots  =  -Coefficient of x²/coefficient of x³

  =  6/2  =  3

a + b + c  =  3

2b + 2c + b + c  =  3

3(b + c)  =  3

b + c  =  1

c = 1 - b

By applying the value of c in a = 2(b + c), we get

a  =  2(b + 1 - b)

a  =  2

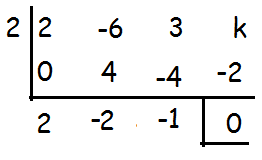
k - 2  =  0

Hence the value of k is 2.

2x² - 2x - 1

x = (-b ± √b² - 4ac)/2a

x = (2 ± √4 + 8)/4

x = (2 ± 2√3)/4

x = (1 ± √3)/2

The required roots are 2, (1 ± √3)/2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.