SOLVING AREA EQUATIONS

The following steps will be useful to solve equations involving area.  

Step 1 :

Draw the picture using the information given in the question (if required). 

Step 2 : 

Write the formula to find the area of the given shape.

Step 3 :

Substitute the given values.

Step 4 :

Using the inverse operations, to solve for the unknown. 

Example 1 :

After winning the state tournament, the wrestling team hangs a pennant shaped like a triangle on the gym wall. The base of the triangle is 1.5 feet long. It has an area of 2.25 square feet. What is the height of the triangle?

Solution :

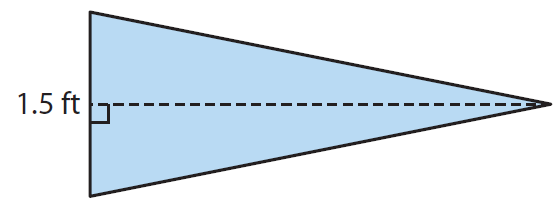
Base of the triangle (b) =  1.5 feet 

Area of the triangle = 2.25 square feet ---(1) 

Area of the triangle = (1/2) x b x h  ---(2) 

By equating the 1st and 2nd equations we get,

(1/2) x b x h = 2.25

(1/2) x 1.5 x h = 2.25

Multiply each side by 2.

1.5 x h = 2.25 x 2

Divide each side by 1.5.

h = 3 feet

Example 2 :

Renee is sewing a quilt whose pattern contains right triangles. Each quilt piece is a right triangle with a height of 6 inches, and an area of 24 square inches. How long is the base of each quilt piece?

Solution :

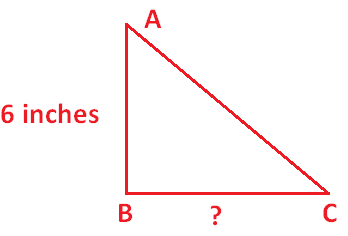
Each quilt piece is in the shape right triangles.

Height of quilt piece = 6 inches

Area of each quilt piece = 24 square inches  ---(1)

Area of right triangle = (1/2) x b x h  ---(2)

(1)  =  (2)

(1/2) x b x 6 = 24 

Simplify. 

b x 3 = 24

Divide each side by 3. 

b  =  8 inches

Example 3 :

A parallelogram shaped field in a park needs sod. The parallelogram has a base of 21.5 meters and a height of 18 meters. The sod is sold in pallets of 50 square meters. How many pallets of sod are needed to fill the field ?

Solution :

Base of parallelogram = 21.5 meters

Height of parallelogram = 18 ft

Area of the field = base x height

=  21.5 x 18

=  387 square meters

The sod is sold in pallets of 50 square meters. 

Number of pallets to fill the field = 387/50 

=  7.74

So, 8 pallets are needed to fill the field.

Example 4 :

Taylor wants to paint his rectangular deck that is 42 feet long and 28 feet wide. A gallon of paint covers about 350 square feet. How many gallons of paint will Taylor need to cover the entire deck?

Solution :

length of rectangular deck = 42 feet

width of rectangular deck = 28 feet

Area of rectangular deck = length x width 

=  42 x 28 

=  1176 square feet

A gallon of paint covers about 350 square feet.

number of gallons of paint will Taylor need to cover the entire deck = 1176 / 350

=  3.36 approximately 4

So, Taylor will need 4 gallons of paint to cover the entire deck.

Example 5 :

A triangular bandana has an area of 70 square inches. The height of the triangle is 8 inches. Write and solve an equation to find the length of the base of the triangle.

Solution :

Area of the triangular bandana = 70 square feet ---(1)

height of the triangle = 8 inches

Area of triangle = (1/2) x b x h  ---(2) 

(1)  =  (2) 

(1/2) x b x 8  =  70

Simplify. 

b x 4  =  80

Divide each side by 4.

b  =  20 feet

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.