SOLVING ABSOLUTE VALUE INEQUALITIES IN INTERVAL NOTATION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
If the given inequalities are in the following form, we may represent the the expression inside the absolute value sign between the range -r and r and solve for x.
|
Given function |
Solution |
|
(i) |x - a| < r (ii) |x - a| > r (iii) |x - a| ≤ r (iv) |x - a| ≥ r |
(a - r, a + r) (∞, a - r) U (a + r, ∞) (∞, a - r] U [a + r , ∞) (∞, a - r] U [a + r, ∞) |
Here, we may have some different cases.
|
Given function |
Solution |
|
|x - a| > -r (or) |x - a| ≥ - r |
Hence the solution is all real numbers. Since we have modulus sign in the left side, always we get positive value as answer. |
|
|x - a| < -r (or) |x - a| ≤ - r |
There is no solution. By applying any positive and negative values for x, we get only positive answer. Because we have modulus sign in the left side. |
Example 1 :
Solve 1/|2x - 1| < 6 and express the solution using the interval notation.
Solution :
Now we have to split the given inequality into two branches.
|
1/(2x-1) > -6 Multiply by 2x - 1 throughout the equation 1 > -6(2x - 1) 1 < -12x + 6 Subtract 6 on both sides 1 - 6 < -12x + 6 - 6 -5 < -12x Divide by -12 on both sides 5/12 > x |
1/(2x-1) < 6 Multiply by 2x - 1 throughout the equation 1 > 6(2x - 1) 1 < 12x - 6 Add 6 on both sides 1 + 6 < 12x - 6 + 6 7 < 12x Divide by 12 on both sides 7/12 < x |
In the last step of first part, we divide -12 throughout the equation. So < sign becomes > sign
Hence the solution in interval notation is (-∞, 5/12) U (7/12, ∞).
Example 2 :
Solve −3|x| + 5 ≤ −2 and graph the solution set in a number line.
Solution :
Let us split the given inequality into two parts
|
−3(x) + 5 ≤ −2 -3x + 5 ≤ −2 Subtract 5 on both sides -3x + 5 - 5 ≤ −2 - 5 -3x ≤ −7 Divide by -3 on both sides x ≥ 7/3 |
−3(-x) + 5 ≤ −2 3x + 5 ≤ −2 Subtract 5 on both sides 3x + 5 - 5 ≤ −2 - 5 3x ≤ −7 Divide by 3 on both sides x ≤ −7/3 |
The interval notation of the above solution is (-∞, -7/3] U [7/3, ∞).
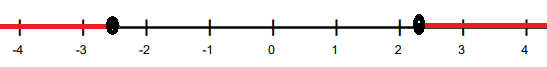
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 18, 26 06:52 PM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
