SOLVE INEQUALITIES

Solve Inequalities :

In this section, we will learn, how to solve an inequality.

An open sentence that contains the symbol <, >, ≤ or ≥  is called an inequality. Inequalities can be solved in the same way as equations.

Difference between equation and inequality

Solving Inequalities - Concept

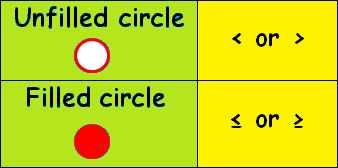
• If we have the inequality < (less than) or > (greater than), we have to use the empty circle.
• If we have the inequality sign ≤ (less than or equal to) or ≥ (greater than or equal to), we have to use the filled circle.

Solve Inequalities - Examples

Example 1 :

Solve each inequality. Then check your solution, and graph it on a number line.

x + 14 ≥ 18

Solution : 

Step 1 :

x + 14 ≥ 18

Subtract 14 on both sides,

x + 14 - 14 ≥ 18 - 14

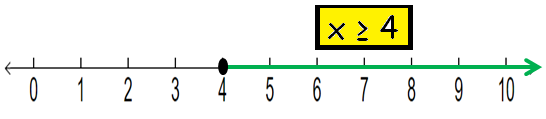
x ≥ 4

Step 2 :

To check the solution, we need to take any values greater than or equal to 4 and check whether it satisfies the condition or not.

Let us take x  =  5

Now we have to apply 5 instead of "x" in the given inequality.

5 + 14 ≥ 18

19 ≥ 18 (True)

Step 3 :

To graph the solution, we have to draw a number line and shade the portion which satisfies the given condition.

Example 2 :

Solve each inequality. Then check your solution, and graph it on a number line.

d + 5 ≤ 7

Solution : 

Step 1 :

d + 5 ≤ 7

Subtract 5 on both sides,

d + 5 - 5 ≤ 7 - 5

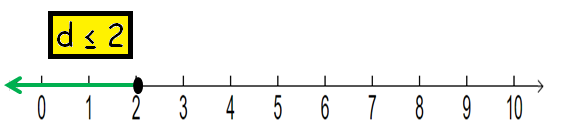
d  ≤ 2

Step 2 :

To check the solution, we need to take any value less than or equal to 2 and check whether it satisfies the condition or not.

Let us take d  =  0

Now we have to apply 0 instead of "d" in the given inequality.

0 + 5 ≤ 7

 5 ≤ 7 (True)

Step 3 :

To graph the solution, we have to draw a number line and shade the portion which satisfies the given condition.

Example 3 :

Solve each inequality. Then check your solution, and graph it on a number line.

-3  ≥  q - 7

Solution : 

Step 1 :

-3  ≥  q - 7

Add 7 on both sides

-3 + 7  ≥  q - 7 + 7

 7  ≥  q 

If we flip the variable to the right side and value to the left side, then we have to change its original sign.

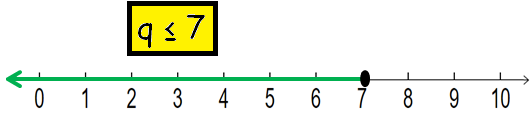
 q ≤ 7 

Step 2 :

To check the solution, we need to take any value lesser than or equal to 7 and check whether it satisfies the condition or not.

Let us take q  =  5

Now we have to apply 5 instead of "q" in the given inequality.

-3  ≥  5 - 7

-3  ≥  - 2 (True)

Step 3 :

To graph the solution, we have to draw a number line and shade the portion which satisfies the given condition.

Example 4 :

Solve each inequality. Then check your solution, and graph it on a number line.

2y  >  -8 + y

Solution : 

Step 1 :

2y  >  -8 + y

Subtract y on both sides

2y - y  >  -8 + y - y

 y  >  -8

Step 2 :

To check the solution, we need to take any value greater than -8.

Let us take y  =  -5

Now we have to apply -5 instead of "y" in the given inequality.

2(-5)  >  -8 - 5

-10 > -13 (True)

Step 3 :

To graph the solution, we have to draw a number line and shade the portion which satisfies the given condition.

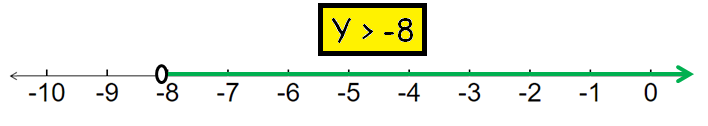
Example 5 :

Solve each inequality. Then check your solution, and graph it on a number line.

3f < -3 + 2f

Solution : 

Step 1 :

3f < -3 + 2f

Subtract 2f on both sides

3f - 2f  <  -3 + 2f - 2f

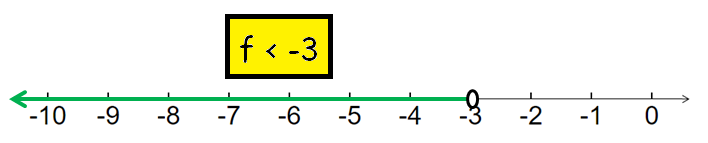
 f  <  -3

Step 2 :

To check the solution, we need to take any value lesser than -2.

Let us take f  =  -2

Now we have to apply -2 instead of "f" in the given inequality.

3(-2) < -3 + 2(-2) 

-6 < -3 - 4 

-6 < -7 (True)

Step 3 :

To graph the solution, we have to draw a number line and shade the portion which satisfies the given condition.

After having gone through the stuff given above, we hope that the students would have understood, how to solve inequalities.  

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.