SOLID MENSURATION PRACTICE PROBLEMS

Problem 1 :

The barrel of a fountain-pen cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen will be used for writing 330 words on an average. How many words can be written using a bottle of ink containing one fifth of a liter?

Solution :

To find the number of words can be written using a bottle of ink, we have to find the quantity of ink in the barrel.

Volume of barrel in the cylindrical shape  =  πr²h

height of shape  =  7 cm

radius of the shape  =  (5/2) mm

10 mm  =  1 cm

(5/2)/10  =  (1/4) cm

Volume of barrel in the cylindrical shape :

  =  (22/7) ⋅ (1/4) (1/4) 7

  =  (11/8) cm³

1000 cm³  =  1 liter

  =  11/8000 liter

Quantity of ink in 1 liter  =  8000/11

Quantity of ink in the bottel =  (1/5) of liter of ink in the barrel

   =  (1/5) (8000/11) 

Number of word written using 1 bottel of ink  =  330

Required number of words  =   (1/5) (8000/11) ⋅ (1/4) 

=  48000 words

Problem 2 :

A hemi-spherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties the tank at the rate of 7 liters per second. How much time will it take to empty the tank completely?

Solution :

To solve this problem, first let us find quantity of water in the tank in liters.

Volume of water in the hemispherical tank  =  (2/3)πr³

  =  (2/3) ⋅ (22/7) ⋅ (1.75)³

  =  (2/3) ⋅ (22/7)  (1.75)  (1.75)  (1.75)

  =  235.81/21

  =  11.22 m³

1 m³  =  1000 liter

=  11.22 (1000) 

=  11220 liters

Quantity of water empties  =   7 liter per second

=  7 (60)

=  420 liter per minute

Time taken to empty the tank  =  11220/420

=  26.71

=  27 minutes (approximately)

Problem 3 :

Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r units.

Solution :

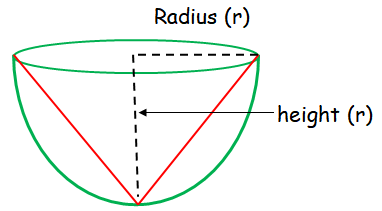
Volume of cone craved out from the hemisphere 

  =  (1/3) r²h

  =  (1/3) r²r

  =  (1/3) r³

Problem 4 :

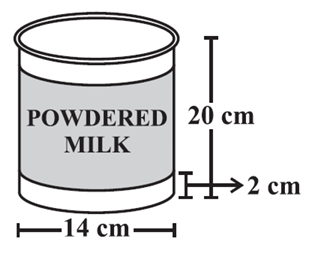
A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in figure). If the label is placed 2 cm from top and bottom, what is the area of the label?

Solution :

Radius = 14/2 ==> 7 cm

Height of the cylindrical shape which is labled

= 20 - (2 + 2)

= 20 - 4

= 16 cm

= 2πrh

= 2 x 3.14 x 7 x 16

= 703.36 cm²

Problem 5 :

A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in liters that can be stored in the tank.

Solution :

Quantity of milk which is stored in the tank = volume of cylinder

= πr²h

radius = 1.5 m, height = 7 m

= 3.14 x 1.5² x 7

= 49.455 m²

Problem 6 :

A cuboidal box of dimensions 1 m × 2 m × 1.5 m is to be painted except its bottom. Calculate how much area of the box has to be painted.

Solution :

Surface area of the box = 2(lw + wh + hl)

length = 1 m, width = 2 m and height = 1.5 m

= 2(1x2 + 2x1.5 + 1.5x1)

= 2(1 + 3 + 1.5)

= 2(5.5)

= 11 m²

Problem 7 :

Water is pouring into a cuboidal reservoir at the rate of 60 liters per minute. If the volume of reservoir is 108 m³, find the number of hours it will take to fill the reservoir.

Solution :

Volume of reservoir = 108 m³

1 m³ = 1000 liter

Converting m³ to liter, we get 108000 liter

Speed of water = 60 liters per minute

1 hour = 60 minute

1 minute = 1/60 hour

60 liter per minute = 60/(1/60)

= 60(60)

= 3600 per hour

= 108000/3600

= 30 hours

So, it will take 30 hours to fill the reservoir.

Problem 8 :

The circumference of the base of the cylindrical vessel is 132 cm, and its height is 25 cm. How many litres of water can it hold? (Assume π = 22/7)

Solution :

Volume of cylinder = πr²h

Circumference of base = 2πr

2πr = 132 cm

2 x (22/7) x r = 132

r = 132 x (7/22) x 1/2

= 21

So, radius of the cylinder is 21 cm.

Capacity of the tank = 3.14 x 21² x 25

= 34618.5 cm³

= 34.6185 liter

Approximately 34.62 liter

Problem 9 :

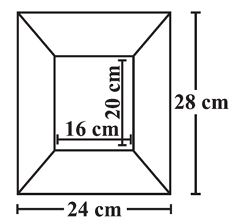
Diagram of the adjacent picture frame has outer dimensions = 24 cm × 28 cm and inner dimensions 16 cm × 20 cm. Find the area of each section of the frame, if the width of each section is same.

Solution :

Area of left and right faces = 1/2 x h x (a + b)

= (1/2) x 16 x (20 + 28)

= 8 x 48

= 384 cm²

= 2(384)

= 768 cm²

Area of top and bottom faces = (1/2) x 20 x (16 + 24)

= 10 x 40

= 400 cm²

= 2 x 400

= 800 cm²

Area of rectangular face = 16 x 20

= 320 cm²

Total area = 768 + 800 + 320

= 1888 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.