SLOPE OF A LINE PERPENDICULAR TO X AXIS

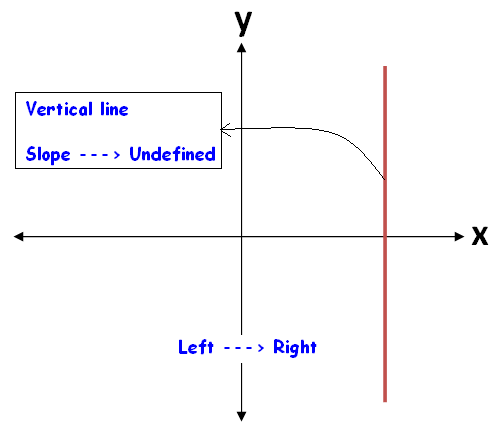
To understand the slope of a line perpendicular to x axis, let us consider the figure given below.

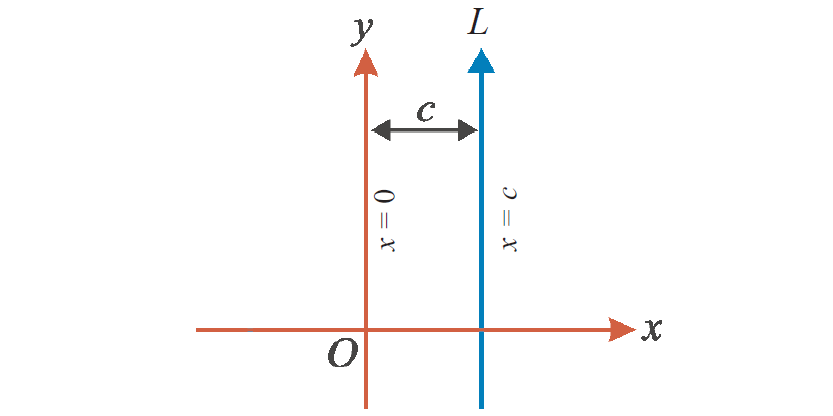
In the figure given above,  the line x = c is perpendicular to  x - axis.

We know that slope  =  change in y / change in x 

In the line x = c, the value of "x" is fixed and that is "c"

So, there is no change in "x" and change in x = 0 

Slope  =  change in y / 0  

Slope  =  Undefined

Apart from slope of a line perpendicular to x axis, let us look at some basic stuff about slope of a line. 

Slope of a Line :

It is the change in y for a unit change in x along the line and usually denoted by the letter "m"

Slope is sometimes referred to as "Rise over run"

Because the fraction consists of the "rise" (the change in y, going up or down) divided by the "run" (the change in x, going from left to the right).

The figure given below illustrates this. 

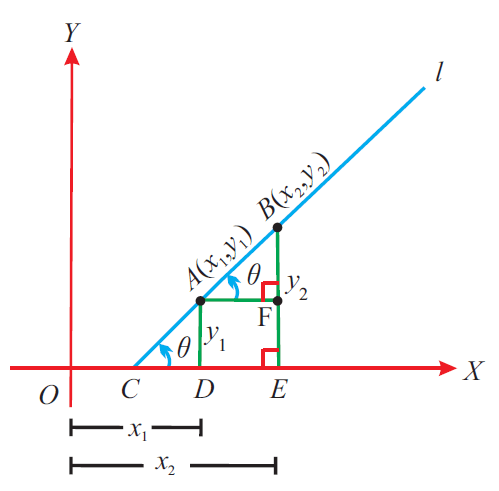
From the above figure, the slope of the straight line joining the points A (x₁, y₁) and B (x₂, y₂) is   

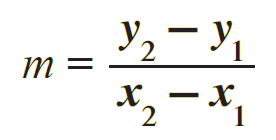
That is, 

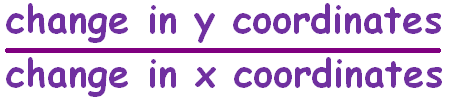
If the equation of a straight line given in general form

ax + by + c  =  0,   

then, the formula to find slope of the line is 

Let θ be the angle between the straight line "l" and the positive side of x - axis.

The figure given below illustrates this. 

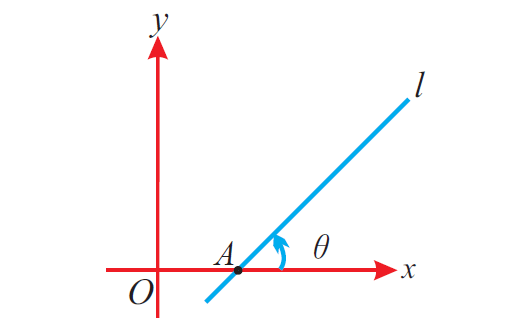
Then, the formula to find slope of the line is

m  =  tan θ

In the general form of equation of a straight line

ax + by + c  =  0,

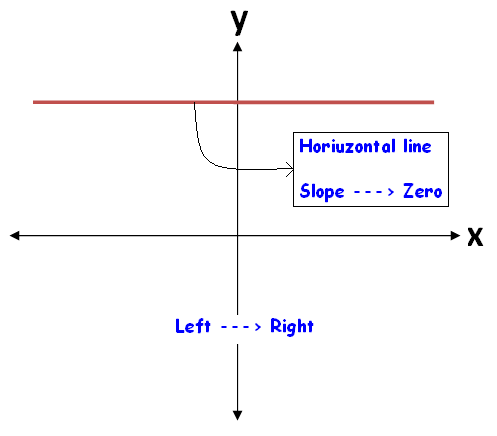
(i)  if "x" term is missing, then the line will be parallel to x - axis and its slope will be zero.

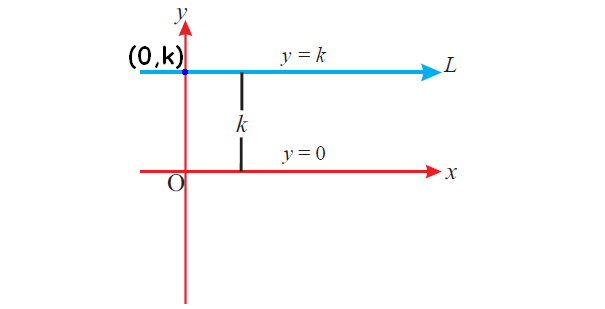
We know that slope  =  change in y / change in x 

In the above figure, the value of "y" is fixed and that is "k"

So, there is no change in "y" and change in y = 0 

Slope  =  0 / change in x  

Slope  =  0

Slope of the coordinate axes "x" and "y". 

(i)  Slope of "x" axis zero.

(ii)  Slope of "y" axis undefined. 

Slope of a line - Positive or Negative or Zero or Undefined

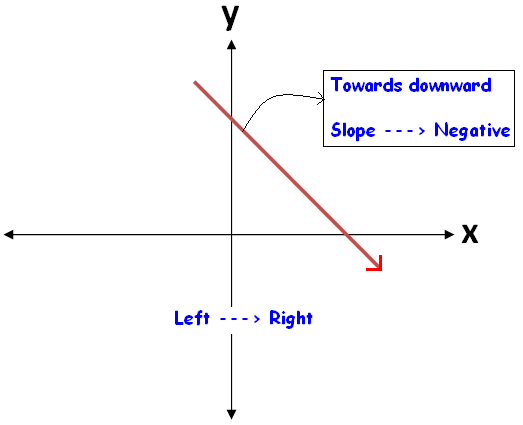
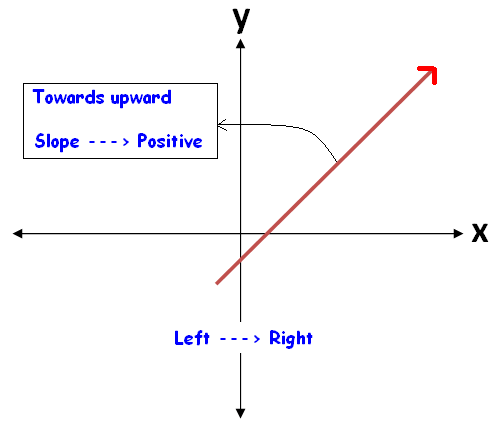
When we look at a straight line visually, we can come to know its slope easily.  

To know the sign of slope of a straight line, always we have to look at the straight line from left to right. 

The figures given below illustrate this. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.