SLOPE INTERCEPT FORM EQUATION OF A LINE WORKSHEET

1. Find the slope-intercept form equation of the straight line with slope 2 and y-intercept 5.

2. Find the slope and y-intercept of the straight line whose equation is 4x - 2y + 1 = 0. 

3. A straight line has the slope 5. If the line cuts y-axis at -2, find the equation of the line in slope-intercept form. 

4. Find the slope-intercept form equation of the straight line passing through the point (-5, -4) with slope 3.

5. Find the equation of the line in slope-intercept form. 

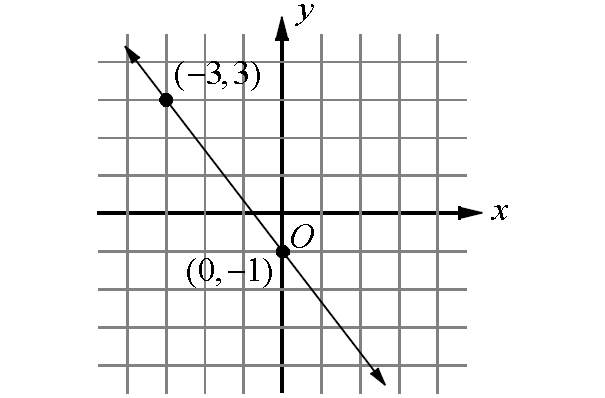
6. Find the slope-intercept form equation of the straight line passing through the point (1, 2) and parallel to the line whose equation is x + 2y + 3 = 0. 

7. Find the slope-intercept form equation of the straight line passing through the point (-2, 3) and perpendicular to the line whose equation is x - 2y - 6 = 0. 

8. A manufacturer produces 80 units of a particular product at a cost of $ 220000 and 125 units at a cost of $ 287500. Assuming the cost curve to be linear, find the cost of 95 units. 

1. Answer :

Given : Slope = 2 and y-intercept form = 5.

Equation of the straight line in slope-intercept form : 

y = mx + b

Substitute m = 2 and b = 5.

y = 2x + 5

2. Answer :

Write the given equation 4x - 2y + 1 = 0 in slope-intercept form. 

4x - 2y + 1 = 0

4x + 1 = 2y

Divide each side by 2. 

(4x + 1)/2 = y

2x + 1/2 = y

or

y = 2x + 1/2

The above form is slope intercept form. 

If we compare y = 2x + 1/2  and  y = mx + b,  we get  

m = 2 and b = 1/2

3. Answer :

Because the line cuts y-axis at -2, clearly y-intercept is -2.

Now, we know that slope m = 5 and y-intercept b = -2.

Equation of a straight line in slope-intercept form is

y = mx + b

Substitute m = 5 and b = -2.

y = 5x - 2

4. Answer :

Equation of the straight line in slope-intercept form.

y = mx + b

Substitute m = 2/3.   

y = 3x + b -----(1)

Given : The line is passing through the point (-5, -4).

Then, 

-4 = 3(-5) + b

-4 = -15 + b

Add 15 to each side. 

11 = b

Substitute b = 11 in (1). 

y = 3x + 11

5. Answer :

The above line is a falling line. So, its slope will be a negative value.

Measure the rise and run. 

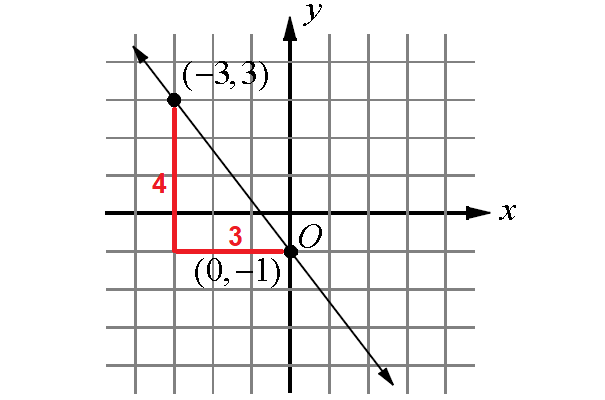
For the above line, rise = 4 and run = 3

slope = rise/run

= -4/3

The line in the diagram above intersects y-axis at -1. 

So, y-intercept is -1. 

Equation of the line in slope intercept form : 

y = mx + b

Substitute -4/3 for m and -1 for b. 

y = -4x/3 - 1

6. Answer :

Write the equation of the line x + 2y + 3 = 0 in slope intercept form. 

x + 2y + 3 = 0

2y = -x - 3

y = (-1/2)x - 3/2

Because the required line is parallel to the given line, the slopes are equal. 

Then, slope of the required line is -1/2.

So, equation of the required line in slope-intercept form is 

y = (-1/2)x + b ----(1)

Given : The line is passing through the point (1, 2).

(1)----> 2 = (-1/2)(1) + b

2 = -1/2 + b

Add 1/2 to each side. 

2 + 1/2 = b

5/2 = b

Substitute b = 5/2 in (1). 

(1)----> y = (-1/2)x + 5/2

7. Answer :

Write the equation of the line x - 2y - 6 = 0 in slope intercept form.  

x - 2y - 6 = 0

-2y = -x + 6

2y = x - 6

y = (1/2)x - 3

So, slope of the given line is 1/2.

Because the required line is perpendicular to the given line, product of the slopes is equal to -1. 

Let 'm' be the slope of the required line. 

m x (1/2) = -1

m/2 = -1

m = -2

So, equation of the required line in slope-intercept form is 

y = -2x + b -----(1)

Given : The line is passing through the point (-2, 3).

(1)----> 3 = -2(-2) + b

3 = 4 + b

Subtract 4 from each side.  

-1 = b

Substitute b = -1 in (1). 

(1)----> y = -2x - 1

8. Answer :

Step 1 :

Since the cost curve is linear, the function which best fits the given information will be a linear-cost function.

y = Ax + B

y ----> Total cost

x ----> Number of units

Step 2 :

Target :

We have to find the value of 'y' for x = 95.

Step 3 :

From the question, we have

x = 80, y = 220000

x = 75, y = 287500

Step 4 :

When we substitute the above values of 'x' and 'y' in

y = Ax + B,

we get 

220000 = 80A + B

287500 = 75A + B

Step 5 :

When we solve the above two linear equations for A and B, we get  

A = 1500, B = 100000

Step 6 :

From A = 1500 and B = 100000, the linear-cost function for the given information is  

y = 1500x + 100000

Step 7 :

To estimate the value of 'y' for x = 95, we have to substitute 95 for x in

y = 1500x + 100000

= 1500 x 95 + 100000

= 142500  +  100000

= 242500

So, the cost of 95 units is $242500.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.