SLOPE AND EQUATION OF A LINE WORKSHEET

Question 1 :

Find the slope of the straight line whose angle of inclination is

(i) 30°       (ii) 60°         (iii) 90°

Question 2 :

Find the slope of the straight line passing through the points

(i) (3, -2) and (7, 2)

(ii) (2, -4) and origin

Question 3 :

Find the slope of the following straight lines

(i) 5y −3  =  0 

(ii) 7x - (3/17)  =  0

Question 4 :

Find the equation of a straight line which has Slope -5/4 and passing through the point (–1, 2).

Question 5 :

Find the equation of a line whose intercepts on the x and y axes are given below.

(i) 4, –6     (ii)  -5, 3/4

Question 6 :

A(-3, 0) B(10, -2) and C(12, 3) are the vertices of triangle ABC . Find the equation of the altitude through A and B.

Answers

1. Answer :

To find slope of the line, when angle of inclination is given

(iii) 90°

m = tan θ

m  =  tan 90

m  =  undefined

2. Answer :

(i) (3 , -2) and (7 , 2)

To find slope of the line passing through two point, we use the formula given below.

(i)  m  =  (y₂ - y₁)/(x₂ - x₁)

m  =  (2 + 2)/(7 - 3)

m  =  4/4

m  =  1

So, slope of the line passing through the given points is 1.

(ii)  (2 , -4) and (0, 0)

m  =  (0 + 4)/(0 - 2)

m  =  4/(-2)

m  =  -2

So, slope of the line passing through the given points is -2.

3. Answer :

(i) 5y −3 = 0

To find slope of the line from the given equation, we use the formula given below. 

Slope (m)  =  -coefficient of x/coefficient of y

  m  =  0/5

  m  =  0

So, the slope of the given line is 0.

(ii) 7 x - (3/17)  = 0

Slope (m)  =  -coefficient of x/coefficient of y

  =  7/0

  m  = undefined

So, the slope of the given line is undefined.

4. Answer :

Slope  =  -5/4

Equation of the line passing through the point (-1, 2)

To find the equation of the line passing through the given point and slope of the line

y - y₁  =  m(x - x₁)

(y - 2)  =  (-5/4) (x - (-1))

4(y - 2)  =  - 5(x + 1)

4y - 2  =  -5x - 5

5x + 4y - 2 + 5  =  0

5x + 4y + 3  =  0

5. Answer :

x intercept  =  a  =  4

y intercept  =  b  =  -6

(x/a) + (y/b)  =  1

(x/4) + (y/(-6))  =  1

(x/4) - (y/6)  =  1

(6x - 4y)/24  =  1

6x - 4y  =  24

3x - 2y  =  12

(ii)  -5, 3/4

x intercept  =  a  =  -5

y intercept  =  b  =  3/4

(x/a) + (y/b)  =  1

(x/(-5)) + (y/(3/4))  =  1

(-x/5) + (4y/3)  =  1

(-3x + 20y)/15  =  1

-3x + 20y  =  15

3x - 20y + 15  =  0

6. Answer :

A(-3, 0) B(10, -2) and C(12, 3) are the vertices of triangle ABC . Find the equation of the altitude through A and B.

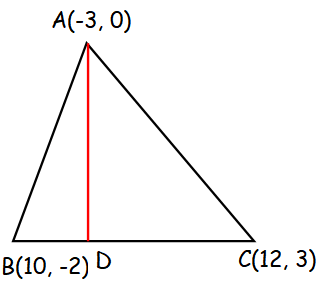
The altitude passing through the vertex A intersect the side BC at D.

AD is perpendicular to BC.

Slope of BC  =  (y₂ - y₁)/(x₂ - x₁)

=  (3 - (-2))/(12 - 10)

=  (3 + 2)/2

=  5/2

Equation of the altitude passing through the vertex A :

(y - y₁)  =  (-1/m)(x - x₁)

A(-3, 0) and m = 5/2

(y - 0)  =  -1/(5/2)(x - (-3))

y = (-2/5) (x + 3)

5y  =  -2x - 6

2x + 5y + 6  =  0

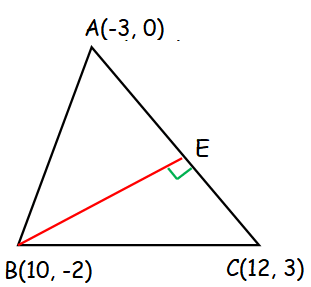
Slope of AC  =  (y₂ - y₁)/(x₂ - x₁)

  =  (3 - 0)/(12 - (-3))

  =  3/(12+3)

  =  3/15

=  1/5

Equation of the altitude passing through the vertex B :

(y - y₁)  =  (-1/m)(x - x₁)

B(10, -2) and m = 1/5

(y - (-2))  =  -1/(1/5)(x - 10)

y + 2  =  -5(x - 10)

y + 2  =  -5x + 50

5x + y + 2 - 50  =  0

5x + y - 48  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.