SKETCHING A TRIANGLE AND DETERMINE THE MEASURE OF INDICATED SIDE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Sketch each triangle. Determine the measure of the indicated side.
Example 1 :
In triangle ABC, ∠A = 57°, ∠B = 73°, and AB = 24 cm. Find the length of AC.
Solution :
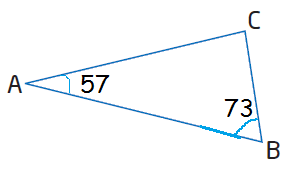
AB = c = 24 cm, BC = a, AC = b, <A = 57 and <B = 73
In triangle ABC,
<A + <B + <C = 180
57 + 73 + <C = 180
<C = 180 - 130 = 50
Using sin formula,
a/sin A = b/sin B = c/sin C
a/sin 57 = b/sin 73 = 24/sin 50
We have to solve for b.
Equating 1 and 3, we get
b/sin 73 = 24/sin 50
b/0.9563 = 24/0.7660
b = 31.33(0.9563)
b = 29.96
b = 30 cm (approximately)
Hence the indicated side is 30 cm.
Example 2 :
In triangle ABC, ∠B = 38°, ∠C = 56°, and BC = 63 cm. Find the length of AB.
Solution :
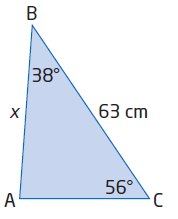
AB = c, BC = a = 63, AC = b, <C = 56 and <B = 38
In triangle ABC,
<A + <B + <C = 180
<A + 38 + 56 = 180
<A = 180 - 94 = 86
Using sin formula,
a/sin A = b/sin B = c/sin C
63/sin 86 = b/sin 38 = c/sin 56
We have to solve for c.
Equating 1 and 3, we get
63/sin 86 = c/sin 56
63/0.9975 = c/0.8290
63.15 = c/0.8290
c = 63.15(0.8290)
c = 52.35
c = 52.4 cm (approximately)
Hence the indicated side is 52.4 cm.
Example 3 :
In triangle ABC, ∠A = 50°, ∠B = 50°, and AC = 27 m. Find the length of AB.
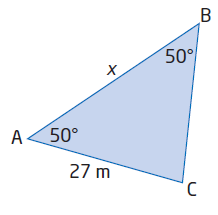
Solution :
AB = c, BC = a = 27 m, AC = b = 27 m, <A = 50 and <B = 50
In triangle ABC,
<A + <B + <C = 180
50 + 50 + <C = 180
<C = 180 - 100 = 80
Using sin formula,
a/sin A = b/sin B = c/sin C
27/sin 50 = 27/sin 50 = c/sin 80
We have to solve for c.
Equating 1 and 3, we get
27/sin 50 = c/sin 80
27/0.7660 = c/0.9848
35.24 = c/0.9848
c = 35.24(0.9848)
c = 34.70 m
Hence the indicated side is 34.7 m.
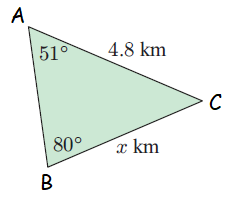
Find the length of the remaining side in the given triangle:
Example 4 :
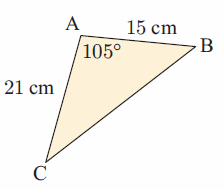
Solution :
The side which is opposite to <A = a, <B = b and <C = c
AB = c = 15 cm, BC = a = ?, AC = b = 21 cm, <CAB = 105
Since we know the two sides and one angle measure, we have to use the cosine rule
a2 = b2 + c2 - 2bc cos A
a2 = 212 + 152 - 2(21)(15) cos 105
= 441 + 225 - 630(-0.25)
= 666 + 157.5
a2 = 823.5
a = √823.5
a = 28.69 cm
Example 5 :
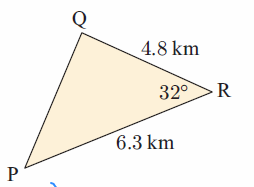
Solution :
The side which is opposite to <P = p, <Q = q and <R = r
QR = p = 4.8 km, PR = q = 6.3 km, PQ = r = ?, <QRP = 32
Since we know the two sides and one angle measure, we have to use the cosine rule
r2 = p2 + q2 - 2pq cos R
r2 = (4.8)2 + (6.3)2 - 2(4.8)(6.3) cos 32
= 23.04 + 39.69 - 60.48 cos 32
= 62.73 - 60.48(0.84)
= 62.73 - 50.80
= 11.93
r = √11.93
r = 3.45 km
Example 6 :
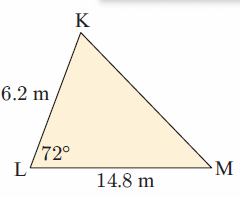
Solution :
The side which is opposite to <K = k, <L = l and <M = m
LM = k = 14.8 m, KM = l = ?, LK = m = 6.2 m, <KLM = ?
Since we know the two sides and one angle measure, we have to use the cosine rule
l2 = k2 + m2 - 2km cos L
l2 = (14.8)2 + (6.2)2 - 2(14.8)(6.2) cos 72
= 219.04 + 38.44 - 183.52 cos 72
= 257.48 - 183.52(0.309)
= 257.48 - 56.70
= 200.78
l = √200.78
l = 14.1 m
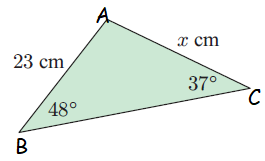
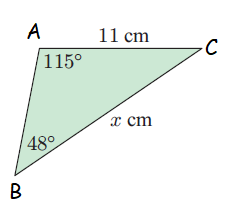
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus BC Problems with Solutions
Dec 20, 25 10:51 AM
AP Calculus BC Problems with Solutions -
AP Precalculus Problems and Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Precalculus Problems and Solutions (Part - 1) -
AP Calculus AB Problems with Solutions (Part - 1)
Dec 20, 25 10:49 AM
AP Calculus AB Problems with Solutions (Part - 1)
