SKETCHING A GRAPH FOR A SITUATION

Graphical representation of a real world situation can be understood better than other forms of representations like textual. Let us see, how to sketch a graph for the given real-world situation. 

Example 1 :

Jacob learned how to spell the same number of words each day.

Sketch a graph for Jacob's learning to spell words. 

Solution : 

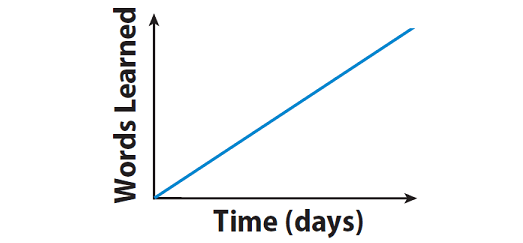
Explanation :

The graph given above shows a constant rate. This means,  Jacob learned how to spell the same number of words each day.

Example 2 :

Micheal started by learning how to spell the same number of words each day but then learned a greater number of words each day.

Sketch a graph for Micheal's learning to spell words. 

Solution : 

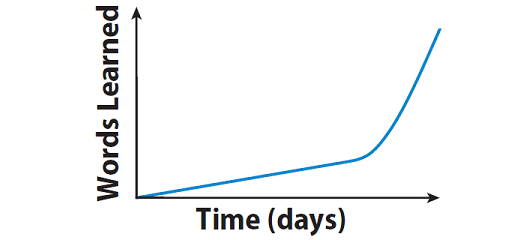
Explanation :

The graph given above begins with a steep curve that gets more shallow. This means, Micheal started by learning how to spell the same number of words each day but then learned a greater number of words each day.

Example 3 :

George started by learning how to spell many words each day but then learned fewer and fewer words each day.

Sketch a graph for George's learning to spell words. 

Solution : 

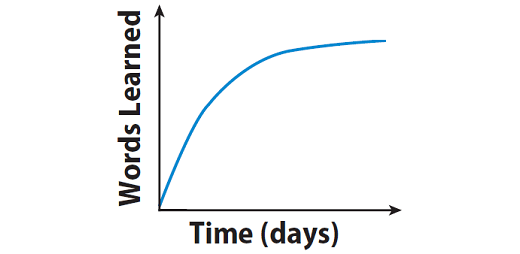
Explanation :

The graph given above begins with a steep curve that gets more shallow. This means, George started by learning how to spell many words each day but then learned fewer and fewer words each day.

Example 4 :

A person steadily increases his speed for some time, then he maintains the constant rate.

Sketch a graph for the above situation.  

Solution : 

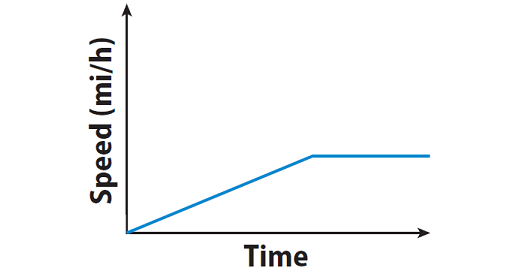
Explanation :

The graph starts with a positive slope and slope becomes zero. This means, the person steadily increases his speed for some time, then he maintains the constant rate. 

Example 5 :

A person begins his ride slowly but then stops to talk with some friends. After a few minutes, he continues his ride, gradually increasing his speed.

Sketch a graph for the above situation.  

Solution : 

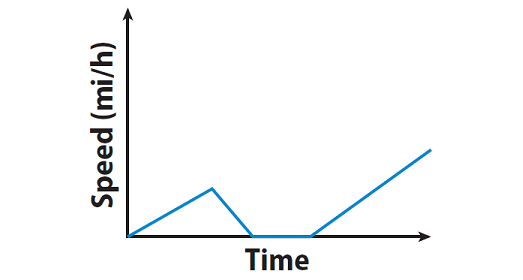
Explanation :

The graph starts with a positive slope, then the slope becomes negative, zero and positive. This means, the person begins his ride slowly but then stops to talk with some friends. After a few minutes, he continues his ride, gradually increasing his speed.

Example 6 :

A person  steadily increases his speed through most of his ride. Then the person A slows down as he nears some trees.

Sketch a graph for the above situation.  

Solution : 

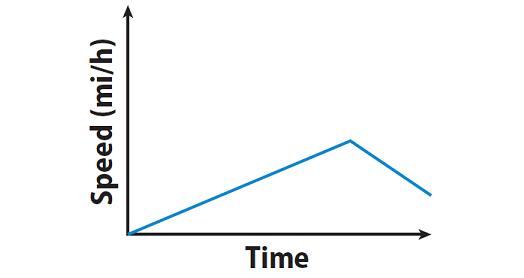
Explanation :

The graph given above starts with a positive slope, then the slope becomes negative. This means, the person  steadily increases his speed through most of his ride. Then the person A slows down as he nears some trees.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.