SKETCH AN ANGLE IN STANDARD POSITION IF TERMINAL ARM PASSES THROUGH A POINT
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Sketch an angle in standard position so that the terminal arm passes through each point.
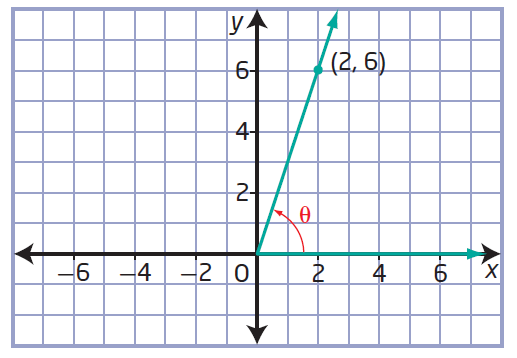
(a) (2, 6)
Solution :
First let us plot the point (2, 6) in the graph paper.
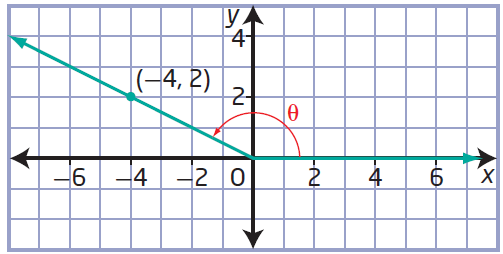
(b) (-4, 2)
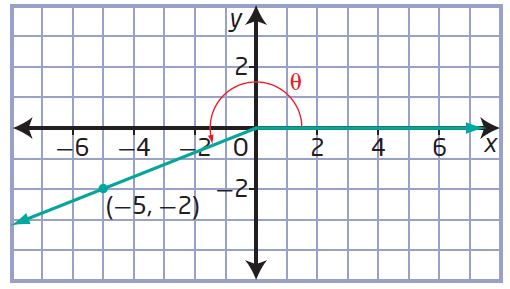
(c) (-5, -2)
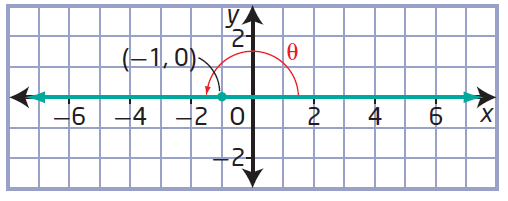
(d) (-1, 0)
Example 2 :
Determine the exact values of the sine, cosine, and tangent ratios for each angle
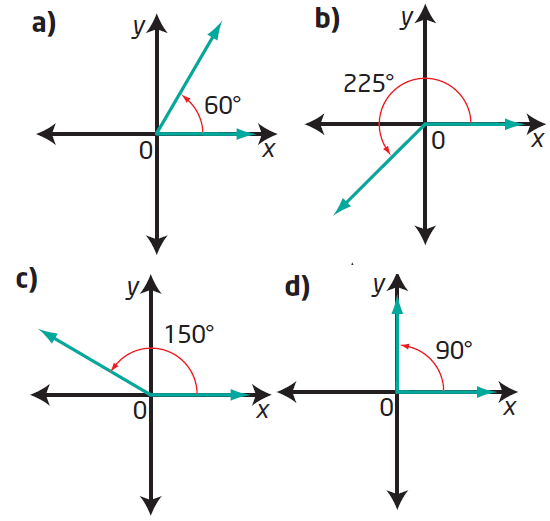
Solution :
By drawing a perpendicular line from A, we get a triangle OAB.
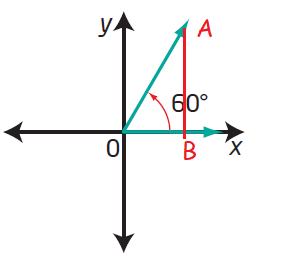
In triangle OAB,
OA = Hypotenuse side
OB = Adjacent side and AB = Opposite side
|
sin 60 = √3/2 |
cos 60 = 1/2 |
tan 60 = √3 |
Since the terminal arm lies in first quadrant, we have to take positive sign for sin 60.
(ii)
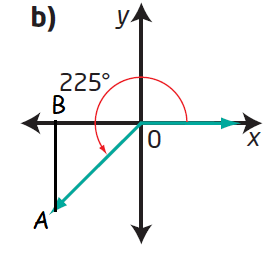
By drawing a perpendicular line from A, we get a triangle OAB.
In triangle OAB,
<BOA = 180 + θ
180 + θ = 225
θ = 225 - 180 = 45
Since the terminal arm lies in the 3rd quadrant, we have to use positive sign for tan and cot only.
|
sin 225 = -1/√2 |
cos 225 = -1/√2 |
tan 225 = 1 |
(iii)
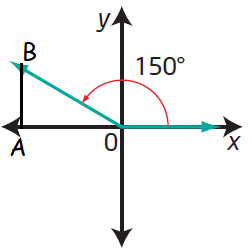
By drawing a perpendicular line from A, we get a triangle OAB.
In triangle OAB,
<AOB = 180 - θ
<AOB = 180 - 150
<AOB = 30
|
sin 150 = 1/2 |
cos 150 = -√3/2 |
tan 150 = -1/√3 |
(iv)
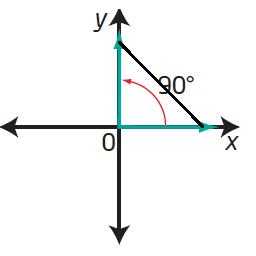
|
sin 90 = 1 |
cos 90 = 0 |
tan 90 = undefined |
Example 3 :
The coordinates of a point P on the terminal arm of each angle are shown. Write the exact trigonometric ratios sin θ, cos θ, and tan θ for each.
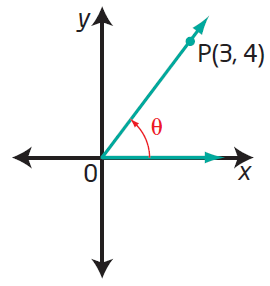
Solution :
Since the terminal arm lies in 3rd quadrant, we have to take positive signs for all trigonometric ratios.
 |
Horizontal length = 3 Vertical length = 4 Hypotenuse = √32 + 42 Hypotenuse = 5 sin θ = 4/5 cos θ = 3/5 tan θ = 4/3 |
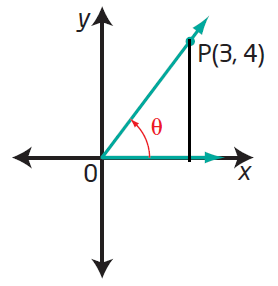
(ii)
Since the terminal arm lies in 3rd quadrant, we have to take positive sign only for tan and cot.
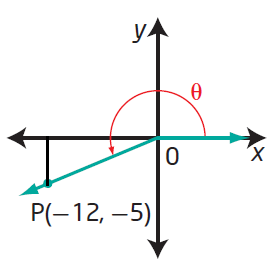 |
Horizontal length = 12 Vertical length = 5 Hypotenuse = √122 + 52 Hypotenuse = 13 sin θ = -5/13 cos θ = -12/13 tan θ = 5/12 |
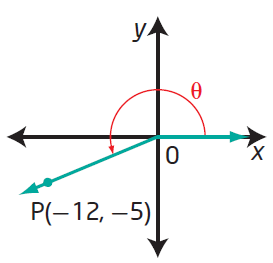
(iii)
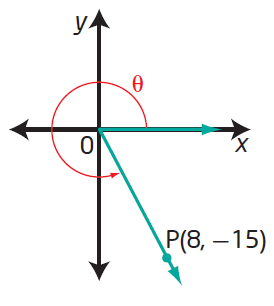
Since the terminal arm lies in 4th quadrant, we have to take positive sign only for cos and sec.
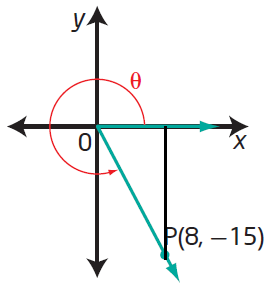 |
Horizontal length = 8 Vertical length = 15 Hypotenuse = √82 + 152 Hypotenuse = 17 sin θ = -15/17 cos θ = 8/17 tan θ = -15/8 |
Example 4 :
a) Plot the given point 𝑃(−4,−5). What quadrant does this point lie in?
b) Construct the corresponding angle in standard position.
c) Drop a perpendicular to the 𝑥-axis creating a right triangle. Which value represents the adjacent side? Which value represents the opposite side?
d) How can you determine the exact length of the hypotenuse?
e) State the cosine, sine and tangent ratios associated with the angle
f) What determines the sign of the ratio? Explain your reasoning.
Solution :
a) Since the given point is in the form of (-x, -y), it will lie in the third quadrant.
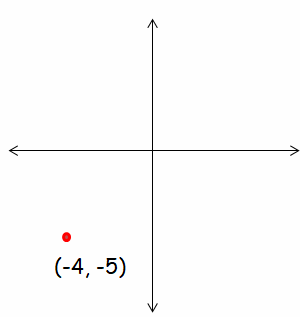
b)
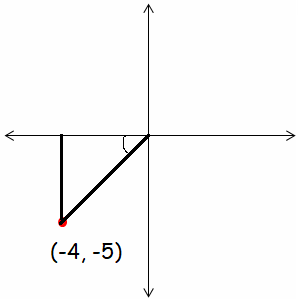
c)
- The side which is opposite to angle measure is opposite side.
- The side which is opposite to angle measure 90 degree is hypotenuse.
- The remaining side is adjacent side.
d)
Horizontal length = adjacent side = 4
Vertical lenght = Opposite side = 5
Hypotenuse = √42 + 52
= √16 + 25
= √41
So, the required hypotenuse is √41
e) sin θ = Opposite side/hypotenuse
cos θ = Adjacent side/hypotenuse
tan θ = Opposite side/adjacent side
f)
Using ASTC, for the trigonometric ratios tan and cot we have positive sign.
sin θ = -4/√41
cos θ = -5/√41
tan θ = -4/(-5) ==> 4/5
Example 5 :
The point P(−3, 4) lies on the terminal arm of an angle, θ, in standard position. Determine the exact trigonometric ratio for cos θ, sin θ and tan θ.
Solution :
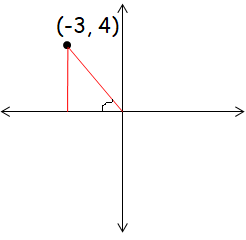
Opposite side = 4
Adjacent side = -3
Hypotenuse = √42 + (-3)2
= √16 + 9
= √25
= 5
Using ASTC, for the trigonometric ratios which lies in the second quadrant sin and cosec we will have positive sign.
sin θ = 4/5
cos θ = -3/5
tan θ = -4/3
Example 6 :
The point P(−8, −15) lies on the terminal arm of an angle, θ, in standard position. Determine the exact trigonometric ratio for cos θ, sin θ and tan θ.
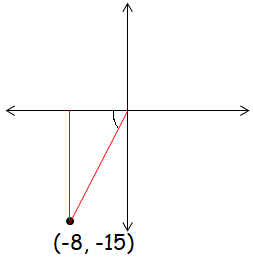
Solution :
Opposite side = -15
Adjacent side = -8
Hypotenuse = √(-15)2 + (-8)2
= √(225 + 64)
= √289
= 17
Using ASTC, for the trigonometric ratios which lies in the third quadrant tan and cot we will have positive sign.
sin θ = -15/17
cos θ = -8/17
tan θ = 15/8
Example 7 :
Suppose θ is an angle in standard position with terminal arm in quadrant III and cos θ = −3/4 . What are the exact values of sin θ and tan θ?
Solution :
cos θ = Adjacent side / hyopotenuse
cos θ = −3/4
Opposite side = √42 - (-3)2
= √(16 - 9)
= √7
Using ASTC, for the trigonometric ratios which lies in the third quadrant tan and cot we will have positive sign.
sin θ = Opposite side/hypotenuse
sin θ = -√7/4
tan θ = opposite side / adjancent side
tan θ = √7/3
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
