SINUSOIDAL FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The general form of a sinusoidal function :
y = a sin [k(x - b)] + N
We can determine following graph properties for plotting one period of sine :
(i) Amplitude = |a| #Note if a < 0, there is a reflection over the x-axis.
(ii) Phase shift/horizontal shift by b #if -b, then right shift by b units. if +b, then left shift by b units.
This is an horizontal stretch or shrink of original sine.
(iii) Plotting Domain for one Period :
(iii) Plotting Domain for one Period :
(iv) x-values for Plotting :
Doing this ensures that you are computing sine of easy values :
(v) Vertical shift : If +N, then we shift the the entire graph N units up. If -N, we shift the entire graph N units down.
Note :
We have the the patterns for the y-values of sin (x).
When there is NO reflection about x-axis :
0, 1, 0, -1, 0
When there is reflection about x-axis :
0, -1, 0, 1, 0
Problem 1 :
y = 4 sin [2(x - π)] + 3
Answer the following questions for the above sinusoidal function.
1. Determine the amplitude of the given function.
2. Is there reflection about the x-axis?
3. Is there a phase shift? If yes, what is this shift?
4. What is the period of the given function :
5. Determine the interval that you should plot over to ensure you plot an entire period.
6. Is there any vertical shift?
Solution :
Comparing
y = a sin [k(x - b)] + N
and
y = 4 sin [2(x - π)] + 3,
we get
a = 4, k =2, b = π and N = 3
Part 1 :
Amplitude = |a|
= |4|
=4
Part 2 :
a = 4 > 0
NO reflection about the x-axis
Part 3 :
Yes, there is a phase shift or horizontal shift
x - b = x - π
π units to the right
Part 4 :
Part 5 :
Part 6 :
Yes, there is a vertical shift
+N = +3
Vertical shift by 3 units up
Problem 2 :
Solution :
Amplitude = 2
NO reflection about the x-axis
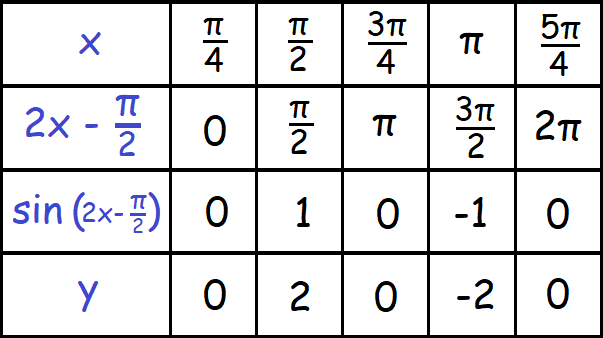
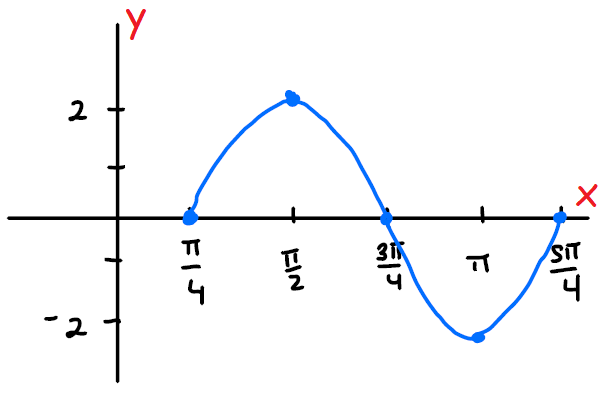
We get the following points from the above table.
Plot the above points on a xy-plane and sketch the graph of the given sinusoidal function.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

