SIMPLIFYING SQUARE ROOTS AND CUBE ROOTS

Find :

Example 1 :

√289

Solution :

Given, √289

We use prime factorization to find square roots.

we get,

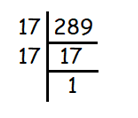
√289  =  √(17 × 17)

For every two same values, we can take one out of them.

=  17

So, the answer is 17

Example 2 :

√441

Solution :

Given, √441

We use prime factorization to find square roots.

We get,

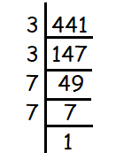
√441  =  √(3 × 3 × 7 × 7)

For every two same values, we can take one out of them.

=  3 × 7

=  21

So, the answer is 21

Example 3 :

√625

Solution :

Given, √625

We use prime factorization to find square roots.

We get,

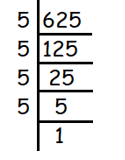
√625  =  √(5 × 5 × 5 × 5)

For every two same values, we can take one out of them.

=  5 × 5

=  25

So, the answer is 25

Example 4 :

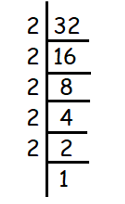
√1024

Solution :

Given, √1024

We use prime factorization to find square roots.

We get,

√1024  =  √(2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2)

For every two same values, we can take one out of them.

=  2 × 2 × 2 × 2 × 2

=  32

So, the answer is 32

Example 5 :

√0

Solution :

Given, √0

√0  =  √0 x 0

Since, square root of zero is zero

So, the answer is 0.

Example 6 :

√1369

Solution :

Given, √1369

We use prime factorization to find square roots.

We get,

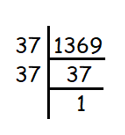
So, the answer is 37

Example 7 :

√6889

Solution :

Given, √6889

We use prime factorization to find square roots.

We get,

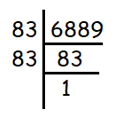
√6889  =  √(83 × 83)

=  83

So, the answer is 83

Example 8 :

√10000

Solution :

Given, √6889

We use prime factorization to find square roots.

We get,

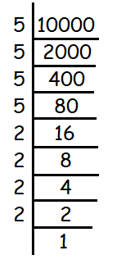
√10000  =  √(5 × 5 × 5 × 5 × 2 × 2 × 2 × 2)

=  5 × 5 × 2 × 2

=  100

So, the answer is 100.

Example 9 :

 ³√1

Solution :

Given, ³√1

³√1  =  ³√(1 x 1 x 1)  ==>  1

So, the answer is 1

Example 10 :

³√64

Solution :

Given, ³√64

We use prime factorization to find cube roots.

We get,

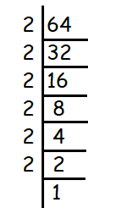
=  ³√(2 × 2 × 2 × 2 × 2 × 2)

=  2 × 2

=  4

So, the answer is 4

Example 11 :

³√125

Solution :

Given, ³√125

We use prime factorization to find cube roots.

We get,

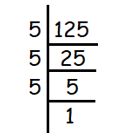
=  ³√(5 × 5 × 5)

For every three same values, we can take one out of them.

=  5

So, the answer is 5

Example 12 :

³√343

Solution :

Given, ³√343

We use prime factorization to find cube roots.

We get,

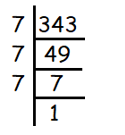
=  ³√(7 × 7 × 7)

=  7

So, the answer is 7

Example 13 :

⁴√0

Solution :

Given, ⁴√0

Since fourth root of 0 is 0

So, the answer is 0

Example 14 :

⁴√16

Solution :

Given, ⁴√16

We use prime factorization to find fourth roots.

We get,

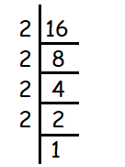
=  ⁴√(2 × 2 × 2 × 2)

For every four same values, we can take one out of them.

=  2

So, the answer is 2

Example 15 :

³√-1

Solution :

Given, ³√-1

Since cube root of - 1 is - 1

So, the answer is – 1

Example 16 :

³√-27

Solution :

Given, ³√-27

We use prime factorization to find cube roots.

We get,

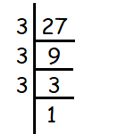
=  ³√(-3) × (-3) × (-3)

=  -3

So, the answer is - 3

Example 17  :

⁴√625

Solution :

Given, ⁴√625

We use prime factorization to find fourth roots.

We get,

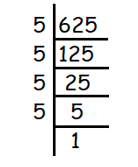
=  ⁴√(5 × 5 × 5 × 5)

=  5

So, the answer is 5

Example 18 :

⁵√1

Solution :

Given, ⁵√1

Since fifth root of 1 is 1

So, the answer is 1

Example 19  :

⁵√-1

Solution :

Given, ⁵√-1

⁵√-1  =  ⁵√(-1) x (-1) x (-1) x (-1) x (-1)

So, the answer is – 1

Example 20 :

⁵√-32

Solution :

Given, ⁵√-32

We use prime factorization to find fifth roots.

We get,

=  ⁵√(-2) × (-2) × (-2) × (-2) × (-2)

=  -2

So, the answer is -2

Example 21 :

9⁷/ ⁴√9¹⁰ = 9^6t, what is the value of t ?

Solution :

9⁷/ ⁴√9¹⁰ = 9^6t

9⁷/ (9¹⁰) ^1/4 = 9^6t

9⁷/ 9 ^5/2 = 9^6t

9^{7 - 5/2} = 9^6t

9^{(14 - 5)/2} = 9^6t

9^(9/2) = 9^6t

Since we have same bases on both sides of the equal sign, we can equate the powers, we get

9/2 = 6t

t = (9/12)

t = 3/4

Example 22 :

2^x-3 - 2^x = k(2^x ), what is the value of k ?

Solution :

2^x-3 - 2^x = k(2^x )

2^x/2³  - 2^x = k(2^x )

Factoring 2^x, we get

2^x(1/2³  - 1) = k(2^x )

1/8 - 1 = k

k = -7/8

So, the value of k is -7/8.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.