SIMPLIFYING SQUARE ROOTS AND CUBE ROOTS WORKSHEET

Find :

Problem 1 :

√289

Solution :

Given, √289

We use prime factorization to find square roots.

we get,

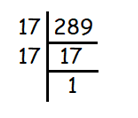
√289  =  √(17 × 17)

For every two same values, we can take one out of them.

=  17

So, the answer is 17

Problem 2 :

√441

Solution :

Given, √441

We use prime factorization to find square roots.

We get,

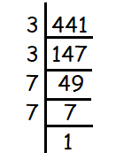
√441  =  √(3 × 3 × 7 × 7)

For every two same values, we can take one out of them.

=  3 × 7

=  21

So, the answer is 21

Problem 3 :

√625

Solution :

Given, √625

We use prime factorization to find square roots.

We get,

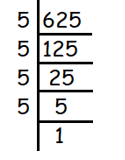
√625  =  √(5 × 5 × 5 × 5)

For every two same values, we can take one out of them.

=  5 × 5

=  25

So, the answer is 25

Problem 4 :

√1024

Solution :

Given, √1024

We use prime factorization to find square roots.

We get,

√1024  =  √(2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2)

For every two same values, we can take one out of them.

=  2 × 2 × 2 × 2 × 2

=  32

So, the answer is 32

Problem 5 :

√0

Solution :

Given, √0

√0  =  √0 x 0

Since, square root of zero is zero

So, the answer is 0.

Problem 6 :

√1369

Solution :

Given, √1369

We use prime factorization to find square roots.

We get,

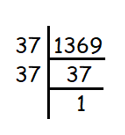
So, the answer is 37

Problem 7 :

√6889

Solution :

Given, √6889

We use prime factorization to find square roots.

We get,

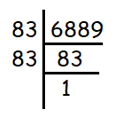
√6889  =  √(83 × 83)

=  83

So, the answer is 83

Problem 8 :

√10000

Solution :

Given, √6889

We use prime factorization to find square roots.

We get,

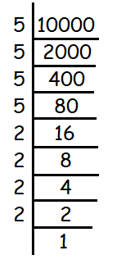
√10000  =  √(5 × 5 × 5 × 5 × 2 × 2 × 2 × 2)

=  5 × 5 × 2 × 2

=  100

So, the answer is 100.

Problem 9 :

 ³√1

Solution :

Given, ³√1

³√1  =  ³√(1 x 1 x 1)  ==>  1

So, the answer is 1

Problem 10 :

³√64

Solution :

Given, ³√64

We use prime factorization to find cube roots.

We get,

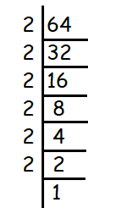
=  ³√(2 × 2 × 2 × 2 × 2 × 2)

=  2 × 2

=  4

So, the answer is 4

Problem 11 :

³√125

Solution :

Given, ³√125

We use prime factorization to find cube roots.

We get,

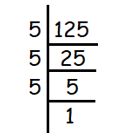
=  ³√(5 × 5 × 5)

For every three same values, we can take one out of them.

=  5

So, the answer is 5

Problem 12 :

³√343

Solution :

Given, ³√343

We use prime factorization to find cube roots.

We get,

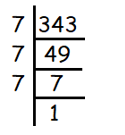
=  ³√(7 × 7 × 7)

=  7

So, the answer is 7

Problem 13 :

⁴√0

Solution :

Given, ⁴√0

Since fourth root of 0 is 0

So, the answer is 0

Problem 14 :

⁴√16

Solution :

Given, ⁴√16

We use prime factorization to find fourth roots.

We get,

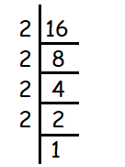
=  ⁴√(2 × 2 × 2 × 2)

For every four same values, we can take one out of them.

=  2

So, the answer is 2

Problem 15 :

³√-1

Solution :

Given, ³√-1

Since cube root of - 1 is - 1

So, the answer is – 1

Problem 16 :

³√-27

Solution :

Given, ³√-27

We use prime factorization to find cube roots.

We get,

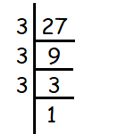
=  ³√(-3) × (-3) × (-3)

=  -3

So, the answer is - 3

Problem 17 :

⁴√625

Solution :

Given, ⁴√625

We use prime factorization to find fourth roots.

We get,

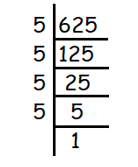
=  ⁴√(5 × 5 × 5 × 5)

=  5

So, the answer is 5

Problem 18 :

⁵√1

Solution :

Given, ⁵√1

Since fifth root of 1 is 1

So, the answer is 1

Problem 19 :

⁵√-1

Solution :

Given, ⁵√-1

⁵√-1  =  ⁵√(-1) x (-1) x (-1) x (-1) x (-1)

So, the answer is – 1

Problem 20 :

⁵√-32

Solution :

Given, ⁵√-32

We use prime factorization to find fifth roots.

We get,

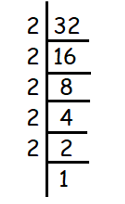
=  ⁵√(-2) × (-2) × (-2) × (-2) × (-2)

=  -2

So, the answer is -2

Problem 21 :

Is 176 a perfect square? If not, find the smallest number by which it should be multiplied to get a perfect square.

Solution :

√176

To check if 176 is a perfect square or not, we have to decompose 176 as prime factors.

√176 = √(2 x 2 x 2 x 11)

Here we see two 2's, in order to make it as pairs, we need one more 2 and one more 11.

= √(2x 2 x 2 x 2 x 11 x 11)

= (2 x 2 x 11)²

22 is smallest number to be multiplied to make 176 as perfect square.

Problem 22 :

Is 9720 a perfect cube? If not, find the smallest number by which it should be divided to get a perfect cube.

Solution :

To check if 9720 is a perfect cube or not, we have to decompose 9720 as prime factors.

³√9720 = ³√(2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 5)

= ³√(2³ x 3⁵ x 5)

= 2 x 3 ³√(3² x 5)

To make it as perfect cube, we need to have one 3 and two 5's.

So, 45 is the least number to be multiplied to make 9720 as perfect cube.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.