SIMPLIFYING RADICALS

Thew following steps will be useful to simplify radicals. 

Step 1 :

Decompose the number inside the radical sign into prime factors.  

Step 2 :

If you have square root (√), you have to take one number out of the square root for every two same numbers multiplied inside the radical.

If you have cube root (³√), we have to take one number out of cube root for every three same numbers multiplied inside the radical.

If you have fourth root (⁴√), you have to take one number out of fourth root for every four same numbers multiplied inside the radical.

Step 3 :

Simplify. 

Examples :

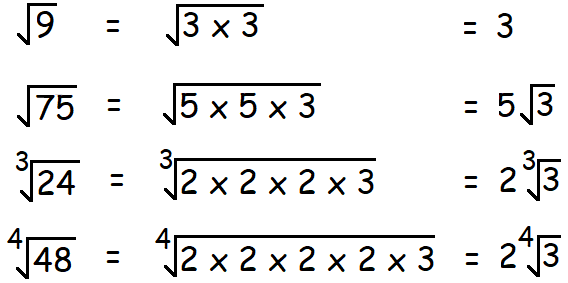
Solved Questions

Question 1 :

Simplify : 

√20

Solution :

Decompose 20 into prime factors using synthetic division. 

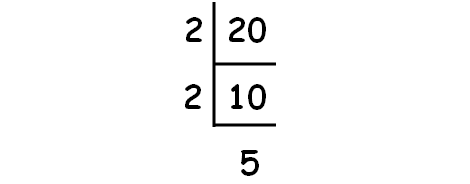
So, we have

√20  =  √(2 ⋅ 2 ⋅ 5)

√20  =  2√5

Question 2 : 

Simplify : 

√121

Solution : 

Decompose 121 into prime factors.

√121  =  √(11 ⋅ 11)

√121  =  11

Question 3 : 

Simplify : 

√52

Solution : 

Decompose 52 into prime factors using synthetic division.

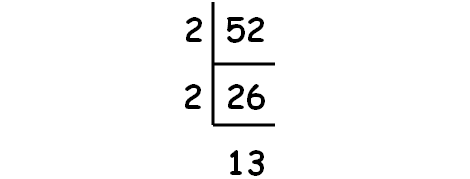
So, we have

√52  =  √(2 ⋅ 2 ⋅ 13)

√52  =  2√13

Question 4 : 

Simplify : 

√45

Solution : 

Decompose 45 into prime factors using synthetic division.

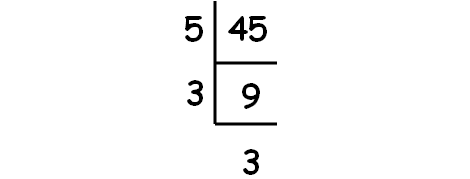
So, we have

√45  =  √(5 ⋅ 3 ⋅ 3)

√45  =  3√5

Question 5 : 

Simplify : 

³√72

Solution : 

Decompose 72 into prime factors using synthetic division.

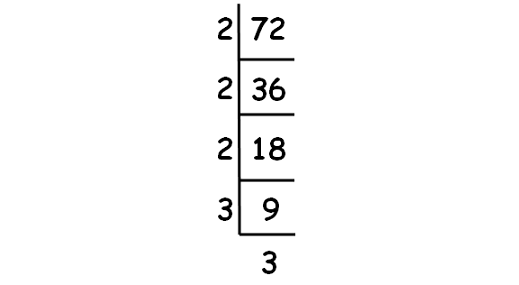
So, we have

³√72  =  ³√(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3)

³√72  =  2 ⋅ ³√(3 ⋅ 3)

³√72  =  2 ⋅ ³√(3 ⋅ 3)

³√72  =  2³√9

Question 6 : 

Simplify : 

 

³√40

Solution : 

Decompose 40 into prime factors using synthetic division.

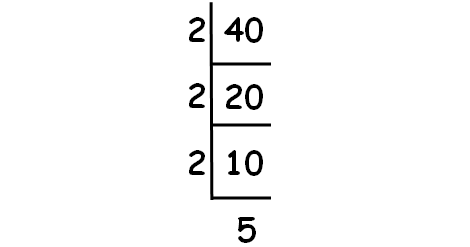
So, we have

³√40  =  ³√(2 ⋅ 2 ⋅ 2 ⋅ 5)

³√40  =  2³√5

Question 7 : 

Simplify : 

³√27

Solution : 

Decompose 27 into prime factors using synthetic division.

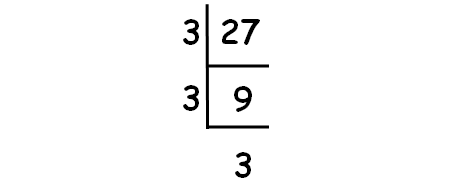
So, we have

³√27  =  ³√(3 ⋅ 3 ⋅ 3)

³√27  =  3

Question 8 : 

Simplify : 

 

⁴√243

Solution : 

Decompose 243 into prime factors using synthetic division.

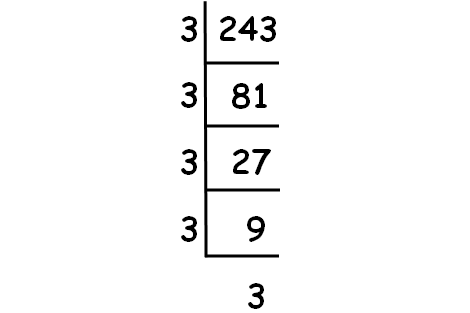
So, we have

⁴√243  =  √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3)

⁴√243  =  3⁴√3

Question 9 : 

Simplify : 

⁵√288

Solution : 

Decompose 288 into prime factors using synthetic division.

So, we have

⁵√288  =  ⁵√(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3)

⁵√288  =  2 ⁵√3

Question 10 : 

Simplify : 

⁶√320

Solution :

Decompose 320 into prime factors using synthetic division.

So, we have

⁶√320  =  ⁶√(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5)

⁶√320  =  2⁶√5

Question 11 :

√12.25 × 18 – (?)² = (6)² + √4

(a) 7     (b) 6    (c) 5    (d) 4    (e) 3

Solution : 

√12.25 × 18 – (?)² = (6)² + √4

√(3.5 x 3.5) × 18 – (?)² = (6)² + √(2 x 2)

3.5 x 18 – (?)² = 36 + 2

63 – (?)² = 38

(?)² = 63 - 38

(?)² = 25

? = √25

? = 5

Question 11 :

√625 ÷ √16 × 6 = ?% of 300

 (a) 15     (b) 12.5     (c) 17.5     (d) 10    (e) 8.5

Solution : 

√625 ÷ √16 × 6 = ?% of 300

√(25 x 25) ÷ √(4 x 4) × 6 = ?% of 300

25 ÷ 4 x 6 = ?% of 300

(25/4) ⋅ 6 = ?% (300)

?% = [(25 ⋅ 6)/4⋅300]

?% = [150/4(300)]

?% = 1/4(2)

?% = 1/8

?% = 0.125

?/100 = 0.125

? = 0.125(100)

?  = 12.5

S, option b is correct.

Question 12 :

√81 × √625 + 1225 = (?)² – 150

(a) 50    (b) 45    (c) 35   (d) 30     (e) 40

Solution : 

√81 × √625 + 1225 = (?)² – 150

√(9 x 9) × √(25 x 25) + 1225 = (?)² – 150

 9 × 25 + 1225 = (?)² – 150

225 + 1225 = (?)² – 150

1450 + 150 =  (?)²

1600 =  (?)²

? =  √1600

? =  √40 x 40

? = 40

 ? = 40

So, option e is correct.

Question 13 :

(2500 + 170 – √4900 ) ÷ 25 + ? = (12)²

(a) 50    (b) 56     (c) 40     (d) 44    e) 39

Solution : 

(2500 + 170 – √4900 ) ÷ 25 + ? = (12)²

(2670 – √(70 x 70) ) ÷ 25 + ? = 144

(2670 – 70) ÷ 25 + ? = 144

2600 ÷ 25 + ? = 144

104 + ? = 144

? = 144 - 104

? = 40

So, option c is correct.

Question 14 :

³√1331 × 343 ÷ 49 − 28 = ?

(a) 55    (b) 49    (c) 62   (d) 42    (e) 39

Solution : 

³√1331 × 343 ÷ 49 − 28 = ?

³√(11 x 11 x 11) × 7 − 28 = ?

 11 × 7 − 28 = ?

77- 28 = ?

? = 49

so, option b is correct.

Question 14 :

√(390 + (√89 + (√121))

(a) 30    (b) 40    (c) 20   (d) 35    (e) 45

Solution :

= √(390 + (√89 + (√121))

= √(390 + (√89 + (√11 x 11))

= √(390 + √(89 + 11)

= √(390 + √100)

= √400

= 20

So, option c is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.