SIMPLIFYING RADICAL EXPRESSIONS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Simplify the radical expression :
√169 + √121
Problem 2 :
Simplify the radical expression :
√20 + √320
Problem 3 :
Simplify the radical expression :
√117 - √52
Problem 4 :
Simplify the radical expression :
√243 - 5√12 + √27
Problem 5 :
Simplify the radical expression :
-√147 - √243
Problem 6 :
Simplify the radical expression :
(√13)(√26)
Problem 7 :
Simplify the radical expression :
(3√14)(√35)
Problem 8 :
Simplify the radical expression :
(8√117) ÷ (2√52)
Problem 9 :
Simplify the radical expression :
(8√3)2
Problem 10 :
Simplify the radical expression :
(√2)3 + √8
Problem 11 :
Simplify the radical expression :
4√(x4/16)
Problem 12 :
Simplify the radical expression :
3√(125p6q3)

Detailed Answer Key
Problem 1 :
Simplify the radical expression :
√169 + √121
Solution :
Decompose 169 and 121 into prime factors using synthetic division.
|
√169 = √(13 ⋅ 13) √169 = 13 |
√121 = √(11 ⋅ 11) √121 = 11 |
So, we have
√169 + √121 = 13 + 11
√169 + √121 = 24
Problem 2 :
Simplify the radical expression :
√20 + √320
Solution :
Decompose 20 and 320 into prime factors using synthetic division.
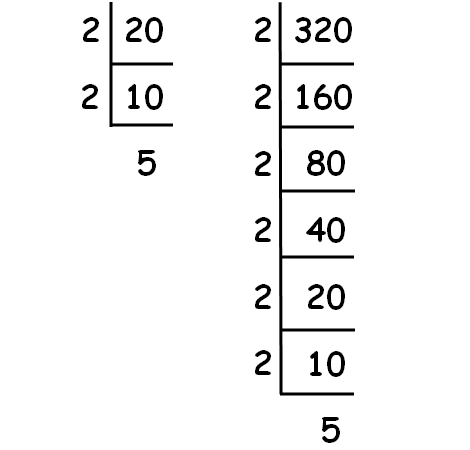
|
√20 = √(2 ⋅ 2 ⋅ 5) √20 = 2√5 |
√320 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5) √320 = 2 ⋅ 2 ⋅ 2 ⋅ √5 √320 = 8√5 |
So, we have
√20 + √320 = 2√5 + 8√5
√20 + √320 = 10√5
Problem 3 :
Simplify the radical expression :
√117 - √52
Solution :
Decompose 117 and 52 into prime factors using synthetic division.
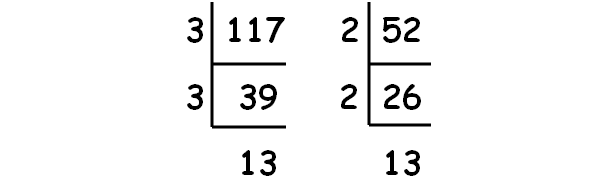
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
So, we have
√117 - √52 = 3√13 - 2√13
√117 + √52 = √13
Problem 4 :
Simplify the radical expression :
√243 - 5√12 + √27
Solution :
Decompose 243, 12 and 27 into prime factors using synthetic division.
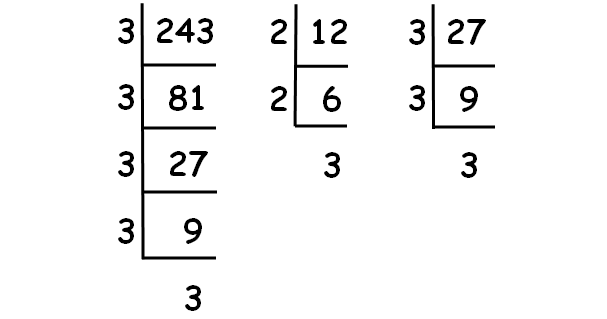
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
√12 = √(2 ⋅ 2 ⋅ 3) = 2√3
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
So, we have
√243 - 5√12 + √27 = 9√3 - 5(2√3) + 3√3
Simplify.
√243 - 5√12 + √27 = 9√3 - 10√3 + 3√3
√243 - 5√12 + √27 = 2√3
Problem 5 :
Simplify the radical expression :
-√147 - √243
Solution :
Decompose 147 and 243 into prime factors using synthetic division.
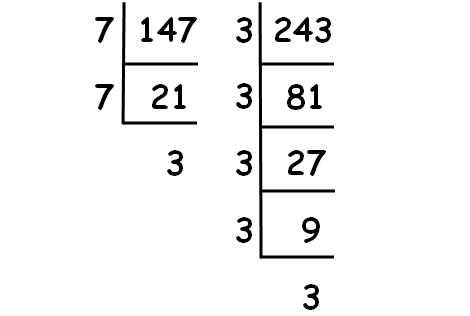
√147 = √(7 ⋅ 7 ⋅ 3) = 7√3
√243 = √(3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3) = 9√3
So, we have
-√147 - √243 = -7√3 - 9√3
-√147 - √243 = -16√3
Problem 6 :
Simplify the radical expression :
(√13)(√26)
Solution :
Decompose 13 and 26 into prime factors.
13 is a prime number. So, it can't be decomposed anymore.
√26 = √(2 ⋅ 13) = √2 ⋅ √13
So, we have
(√13)(√26) = (√13)(√2 ⋅ √13)
(√13)(√26) = (√13 ⋅ √13)√2
(√13)(√26) = 13√2
Problem 7 :
Simplify the radical expression :
(3√14)(√35)
Solution :
Decompose 14 and 35 into prime factors.
√14 = √(2 ⋅ 7) = √2 ⋅ √7
√35 = √(5 ⋅ 7) = √5 ⋅ √7
So, we have
(3√14)(√35) = 3( √2 ⋅ √7)(√5 ⋅ √7)
(3√14)(√35) = 3(√7 ⋅ √7)(√2 ⋅ √5)
(3√14)(√35) = 3(7)√(2 ⋅ 5)
(3√14)(√35) = 21√10
Problem 8 :
Simplify the radical expression :
(8√117) ÷ (2√52)
Solution :
Decompose 117 and 52 into prime factors using synthetic division.
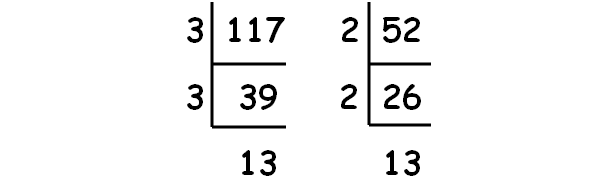
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
(8√117) ÷ (2√52) = 8(3√13) ÷ 2(2√13)
(8√117) ÷ (2√52) = 24√13 ÷ 4√13
(8√117) ÷ (2√52) = 24√13 / 4√13
(8√117) ÷ (2√52) = 6
Problem 9 :
Simplify the radical expression :
(8√3)2
Solution :
(8√3)2 = 8√3 ⋅ 8√3
(8√3)2 = (8 ⋅ 8)(√3 ⋅ √3)
(8√3)2 = (64)(3)
(8√3)2 = 192
Problem 10 :
Simplify the radical expression :
(√2)3 + √8
Solution :
(√2)3 + √8 = (√2 ⋅ √2 ⋅ √2) + √(2⋅ 2 ⋅ 2)
(√2)3 + √8 = (2 ⋅ √2) + 2√2
(√2)3 + √8 = 2√2 + 2√2
(√2)3 + √8 = 4√2
Problem 11 :
Simplify the radical expression :
4√(x4/16)
Solution :
4√(x4/16) = 4√(x4) / 4√16
4√(x4/16) = 4√(x ⋅ x ⋅ x ⋅ x) / 4√(2 ⋅ 2 ⋅ 2 ⋅ 2)
4√(x4/16) = x / 2
Problem 12 :
Simplify the radical expression :
3√(125p6q3)
Solution :
3√(125p6q3) = 3√(5 ⋅ 5 ⋅ 5 ⋅ p2 ⋅ p2 ⋅ p2 ⋅ q ⋅ q ⋅ q)
3√(125p6q3) = 5p2q
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 50)
Mar 06, 26 07:48 PM
Digital SAT Math Problems and Solutions (Part - 50) -
Digital SAT Math Problems and Solutions (Part - 49)
Mar 06, 26 06:47 PM
Digital SAT Math Problems and Solutions (Part - 49) -
Digital SAT Math Problems and Solutions (Part - 48)
Mar 06, 26 05:24 PM
Digital SAT Math Problems and Solutions (Part - 48)


