SIMPLIFYING RADICAL EXPRESSIONS USING CONJUGATES

Key Concept

Case 1 :

If the denominator is in the form of a ± √b or a ± c√b  (where b is a rational number), then we have to multiply both the numerator and denominator by its conjugate.

a + √b and a - √b are conjugate to each other

a + c√b and a - c√b are conjugate to each other

Case 2 :

If the denominator is in the form of √a ± √b (where a and b are rational numbers), then we have to multiply both the numerator and denominator by its conjugate.

√a + √b and √a - √b are conjugate to each other

Radical Conjugate

If the product of two irrational numbers is rational, then  the two irrational numbers are radical conjugate to the other.

Example : 

The product of two irrational numbers √2 and √8 is the rational number 4. 

That is, 

√2 ⋅ √8  =  √(2 ⋅ 8) 

√2 ⋅ √8  =  √16 

√2 ⋅ √8  =  √(4 ⋅ 4)

√2 ⋅ √8  =  4

So, √2 and √8 are radical conjugate to each other. 

Solved Examples

Example 1 :

Simplify : 

1 / (2 + √5)

Solution :

Simplifying the above radical expression is nothing but rationalizing the denominator. 

So, rationalize the denominator. 

Here, the denominator is 2 + √5. 

In the given fraction, multiply both numerator and denominator by the conjugate of 2 + √5. That is 2 - √5.

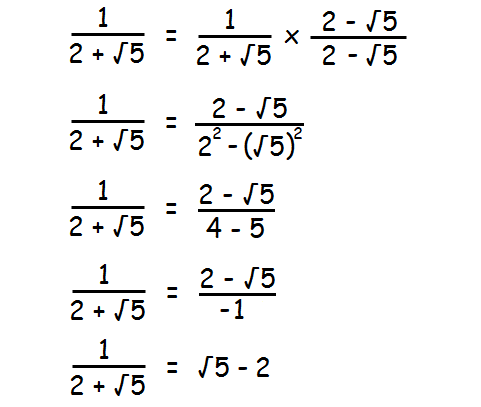
Example 2 :

Simplify :

(6 + √5) / (6 - √5)

Solution :

Simplifying the above radical expression is nothing but rationalizing the denominator. 

So, rationalize the denominator. 

Here, the denominator is 6 - √5. 

In the given fraction, multiply both numerator and denominator by the conjugate of 6 - √5. That is 6 + √5.

(6 + √5) / (6 - √5)  =  [(6+√5)(6+√5)] / [(6-√5)(6+√5)]

(6 + √5) / (6 - √5)  =  [(6+√5)(6+√5)] / [(6-√5)(6+√5)]

(6 + √5) / (6 - √5)  =  (6 + √5)² / [6² - (√5)²]

(6 + √5) / (6 - √5)  =  [6² + 2(6)(√5) + (√5)²] / (36 - 5)

(6 + √5) / (6 - √5)  =  [36 + 12√5 + 5] / 31

(6 + √5) / (6 - √5)  =  (41 + 12√5) / 31

Example 3 :

Simplify : 

1 / (8 - 2√5)

Solution :

Simplifying the above radical expression is nothing but rationalizing the denominator. 

So, rationalize the denominator. 

Here, the denominator is 8 - 2√5. 

In the given fraction, multiply both numerator and denominator by the conjugate of 8 - 2√5. That is 8 + 2√5.

1 / (8 - 2√5)  =  1(8+2√5) / [(8-2√5)(8+2√5)

1 / (8 - 2√5)  =  (8 + 2√5) / [8² - (2√5)²]

1 / (8 - 2√5)  =  (8 + 2√5) / [64 - (4 ⋅ 5]

1 / (8 - 2√5)  =  (8 + 2√5) / [64 - 20]

1 / (8 - 2√5)  =  (8 + 2√5) / 44

1 / (8 - 2√5)  =  2(4 + √5) / 44

1 / (8 - 2√5)  =  (4 + √5) / 22

Example 4 :

Simplify : 

2 / √3

Solution :

Simplifying the above radical expression is nothing but rationalizing the denominator. 

So, rationalize the denominator. 

Here, the denominator is √3. 

In the given fraction, multiply both numerator and denominator by √3.

2 / √3  =  (2√3) / (√3 ⋅ √3)

2 / √3  =  2√3 / 3

Example 5 :

Simplify : 

1/√2  +  1/√5

Solution :

To add the above two fractions, make the denominators same. 

Least common multiple of √2 and √5 is 

=  √2 ⋅ √5

=  √(2 ⋅ 5)

=  √10

Then, 

1/√2  +  1/√5  =  √5/√10  +  √2/√10

1/√2  +  1/√5  =  (√5 + √2) / √10

To rationalize the denominator on the right side, multiply both numerator and denominator by √10.

1/√2  +  1/√5  =  [(√5+√2)√10] / (√10 ⋅ √10)

1/√2  +  1/√5  =  (√50 + √20) / 10

1/√2  +  1/√5  =  (√(5 ⋅ 5 ⋅ 2) + √2 ⋅2 ⋅ 5) / 10

1/√2  +  1/√5  =  (5√5 + 2√5) / 10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.