SIMPLIFYING RADICAL EXPRESSIONS INVOLVING FRACTIONS WORKSHEET

Use the quotient property to write the following radical expression in simplified form. 

(1)
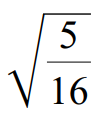(2)
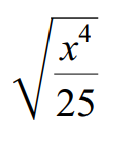(3)
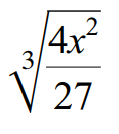(4)
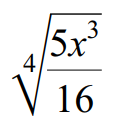(5)
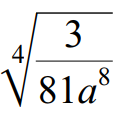(6)
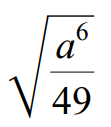(7)
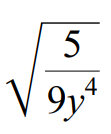(8)

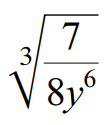Detailed Answer Key

Problem 1 :

Use the quotient property to write the following radical expression in simplified form. 

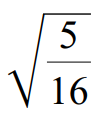
Solution :

√(5/16)  =  √5 / √16

√(5/16)  =  √5 / √(4 ⋅ 4)

Index of the given radical is 2.

Because its index is 2, we can take one term out of radical for every two same terms multiplied inside the radical sign.

√(5/16)  =  √5 / 4

Problem 2 :

Use the quotient property to write the following radical expression in simplified form. 

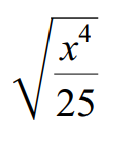
Solution :

√(x⁴/25)  =  √x⁴ / √25

√(x⁴/25)  =  √(x² ⋅ x²) / √(5 ⋅ 5)

Index of the given radical is 2.

Because its index is 2, we can take one term out of radical for every two same terms multiplied inside the radical sign.

√(x⁴/25)  =  x² / 5

Problem 3 :

Use the quotient property to write the following radical expression in simplified form. 

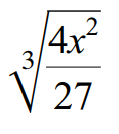
Solution :

³√(4x²/27)  =  ³√4x² / ³√27

³√(4x²/27)  =  ³√(4x²) / ³√(3 ⋅ 3 ⋅ 3)

Index of the given radical is 3.

Because its index is 3, we can take one term out of radical for every three same terms multiplied inside the radical sign.

³√(4x²/27)  =  ³√(4x²) / 3

Problem 4 :

Use the quotient property to write the following radical expression in simplified form. 

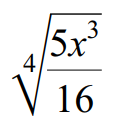
Solution :

⁴√(5x³/16)  =  ⁴√(5x³) / ⁴√16

⁴√(5x³/16)  =  ⁴√5x³ / ⁴√(2 ⋅ 2  ⋅ 2 ⋅ 2)

Index of the given radical is 4.

Because its index is 4, we can take one term out of the radical for every four same terms multiplied inside the radical sign. 

⁴√(5x³/16)  =  ⁴√5x³ / 2

Problem 5 :

Use the quotient property to write the following radical expression in simplified form. 

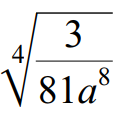
Solution :

⁴√(3/81a⁸)  =  ⁴√3 / ⁴√(81a⁸)

⁴√(3/81a⁸)  =  ⁴√3 / ⁴√(3a² ⋅ 3a² ⋅ 3a² ⋅ 3a²) 

Index of the given radical is 4.

Because its index is 4, we can take one term out of the radical for every four same terms multiplied inside the radical sign. 

⁴√(3/81a⁸)  =  ⁴√3 / 3a²

Problem 6 :

Use the quotient property to write the following radical expression in simplified form. 

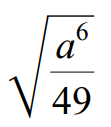
Solution :

√(a⁶/49)  =  √a⁶/√49

√(a⁶/49)  =  √(a³ ⋅ a³)/(7 ⋅ 7)

Index of the given radical is 2.

Because its index is 2, we can take one term out of the radical for every two same terms multiplied inside the radical sign. 

√(a⁶/49)  =  a³/7

Problem 7 :

Use the quotient property to write the following radical expression in simplified form. 

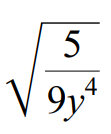
Solution :

√(5/9y⁴)  =  √5 / √9y⁴

√(5/9y⁴)  =  √5 / (3y² ⋅ 3y²)

Index of the given radical is 2.

Because its index is 2, we can take one term out of the radical for every two same terms multiplied inside the radical sign. 

√(5/9y⁴)  =  √5 / 3y²

Problem 8 :

Use the quotient property to write the following radical expression in simplified form. 

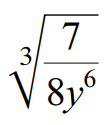
Solution :

³√(7/8y⁶)  =  ³√7 / ³√(8y⁶)

³√(7/8y⁶)  =  ³√7 / ³√(2y² ⋅ 2y² ⋅ 2y²)

Index of the given radical is 3.

Because its index is 3, we can take one term out of the radical for every three same terms multiplied inside the radical sign. 

³√(7/8y⁶)  =  ³√7 / 2y²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.