SIMPLIFYING RADICAL EXPRESSIONS BY RATIONALIZING THE DENOMINATOR

Example 1 :

Simplify : 

18 / √6

Solution :

Simplifying the above radical expression is nothing but rationalizing the denominator. 

So, rationalize the denominator. 

Here, the denominator is √6. 

In the given fraction, multiply both numerator and denominator by √6.

18 / √6  =  (18√6) / (√6 ⋅ √6)

18 / √6  =  18√6 / 6

18 / √6  =  3√6

Example 2 :

Simplify : 

1 / (2 + √5)

Solution :

Simplifying the above radical expression is nothing but rationalizing the denominator. 

So, rationalize the denominator. 

Here, the denominator is 2 + √5. 

In the given fraction, multiply both numerator and denominator by the conjugate of 2 + √5. That is 2 - √5.

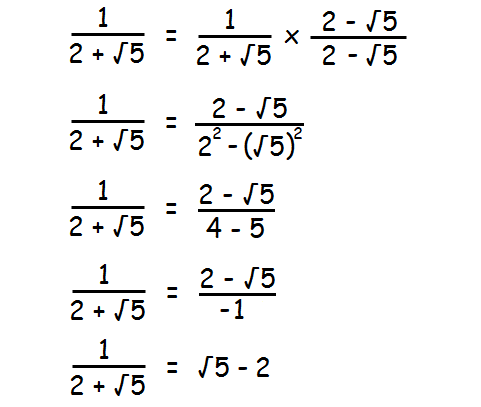
Example 3 :

Simplify :

(6 + √5) / (6 - √5)

Solution :

Simplifying the above radical expression is nothing but rationalizing the denominator. 

So, rationalize the denominator. 

Here, the denominator is 6 - √5. 

In the given fraction, multiply both numerator and denominator by the conjugate of 6 - √5. That is 6 + √5.

(6 + √5) / (6 - √5)  =  [(6+√5)(6+√5)] / [(6-√5)(6+√5)]

(6 + √5) / (6 - √5)  =  [(6+√5)(6+√5)] / [(6-√5)(6+√5)]

(6 + √5) / (6 - √5)  =  (6 + √5)² / [6² - (√5)²]

(6 + √5) / (6 - √5)  =  [6² + 2(6)(√5) + (√5)²] / (36 - 5)

(6 + √5) / (6 - √5)  =  [36 + 12√5 + 5] / 31

(6 + √5) / (6 - √5)  =  (41 + 12√5) / 31

Example 4 :

Find the values of 'x' and 'y' :

(2 + √3)/(2 - √3)  =  x + y√3

Solution : 

(2 + √3)/(2 - √3)  =  x + y√3

On the left side of the above equation, multiply both numerator and denominator by the conjugate of 2 - √3. That is 2 + √3.

[(2+√3)(2+√5)] / [(2-√3)(2+√3)]  =  x + y√3

(2 + √3)² / [2² - (√3)²]  =  x + y√3

[2² + 2(2)(√3) + (√3)²] / (4 - 3)  =  x + y√3

[4 + 4√3 + 3] / 1  =  x + y√3

7 + 4√3  =  x + y√3

Therefore, 

x  =  7

y  =  4

Example 5 :

Simplify :

√(12x²) / √(30x)

Solution : 

√(12x²) / √(30x)  =  √(12x²/30x)

√(12x²) / √(30x)  =  √(2x/5)

√(12x²) / √(30x)  =  √(2x) / √5

On the right side, multiply both numerator and denominator by √5.

√(12x²) / √(30x)  =  √(2x) ⋅ √5 / √5 ⋅ √5

√(12x²) / √(30x)  =  √(2x ⋅ 5) / 5

√(12x²) / √(30x)  =  √10x / 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.