SIMPLIFYING QUOTIENTS OF RADICALS WORKSHEET

Problem 1 :

Simplify the quotient : 

6 / √5

Problem 2 :

Simplify the quotient : 

2√3 / √6

Problem 3 :

Simplify the quotient : 

√18 / (3√2)

Problem 4 : 

Simplify the quotient : 

√5 / √10

Problem 5 : 

Simplify the quotient : 

9 / √72

Detailed Answer Key

Problem 1 :

Simplify the quotient : 

6 / √5

Solution : 

Multiply both numerator and denominator by √5 to get rid of the radical in the denominator.  

6 / √5  =  (6/√5) ⋅ (√5/√5)

6 / √5  =  6√5 / 5

Problem 2 :

Simplify the quotient : 

2√3 / √6

Solution : 

Simplify.

2√3/√6  =  2√3 / (√2 ⋅ √3)

2√3/√6  =  2 / √2

On the right side, multiply both numerator and denominator by √2 to get rid of the radical in the denominator.  

2√3/√6  =  (2/√2) ⋅ (√2/√2)

2√3/√6  =  2√2 / (√2 ⋅ √2)

2√3/√6  =  2√2 / 2

2√3/√6  =  √2

Problem 3 :

Simplify the quotient : 

√18 / (3√2)

Solution :

Simplify.

√18 / (3√2)  =  √(3 ⋅ 3 ⋅ 2) / (3√2)

√18 / (3√2)  =  3√2 / (3√2)

√18 / (3√2)  =  1

Problem 4 : 

Simplify the quotient : 

√5 / √10

Solution :

Simplify.

√5 / √10  =  √5 / √(5 ⋅ 2)

√5 / √10  =  √5 / (√5 ⋅ √2)

√5 / √10  =  1 / √2

On the right side, multiply both numerator and denominator by √2 to get rid of the radical in the denominator.  

√5 / √10  =  (1/√2) ⋅ (√2/√2)

√5 / √10  =  √2 / 2

Problem 5 : 

Simplify the quotient : 

9 / √72

Solution :

Decompose 72 into prime factor using synthetic division. 

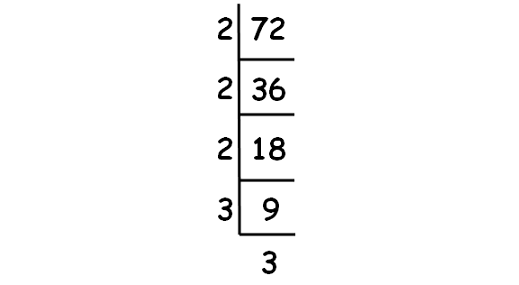
√72  =  √(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3)

√72  =  2 ⋅ 3 ⋅ √2

√72  =  6√2

Then, we have

9 / √72  =  9 / 6√2

Simplify. 

9 / √72  =  3 / 2√2

On the right side, multiply both numerator and denominator by √2 to get rid of the radical in the denominator.  

9 / √72  =  (3/2√2) ⋅ (√2/√2)

9 / √72  =  3√2 / (2√2 ⋅ √2)

9 / √72  =  3√2 / 4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.