SIMPLIFY RADICAL EXPRESSIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In this section, you will learn how to simplify radical expressions.
Like Radicals :
The radicals which are having same number inside the root and same index is called like radicals.
Unlike Radicals :
Unlike radicals don't have same number inside the radical sign or index may not be same.
We can add and subtract like radicals only.
The following steps will be useful to simply radical expressions
Step 1 :
Decompose the number inside the radical sign into prime factors.
Step 2 :
Take one number out of the radical for every two same numbers multiplied inside the radical sign, if the radical is a square root.
Take one number out of the radical for every three same numbers multiplied inside the radical sign, if the radical is a cube root.
Step 3 :
Simplify.
Examples :
√4 = √(2 ⋅ 2) = 2
√16 = √(2 ⋅ 2 ⋅ 2 ⋅ 2) = 2 ⋅ 2 = 2
3√27 = 3√(3 ⋅ 3 ⋅ 3) = 3
3√125 = 3√(5 ⋅ 5 ⋅ 5) = 5
Question 1 :
Simplify :
√20 - √225 + √80
Solution :
Decompose 20, 225 and 80 into prime factors using synthetic division.
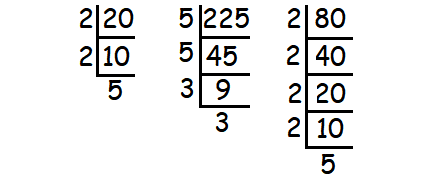
√20 = √2 ⋅ 2 ⋅ 5 = 2√5
√225 = √5 ⋅ 5 ⋅ 3 ⋅ 3 = 5 ⋅ 3 = 15
√225 = √2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5 = (2 ⋅ 2)√5 = 4√5
Then, we have
√20 - √225 + √80 = 2√5 - 15 + 4√5
√20 - √225 + √80 = 6√5 - 15
√20 - √225 + √80 = 6√5 - 15
√20 - √225 + √80 = 3(2√5 - 5)
Question 2 :
Simplify :
√27 + √75 + √108 - √48
Solution :
Decompose 27, 75, 48 and 108 into prime factors using synthetic division.
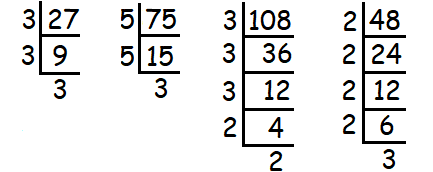
√27 = √(3 ⋅ 3 ⋅ 3) = 3√3
√75 = √(5 ⋅ 5 ⋅ 3) = 5√3
√108 = √(3 ⋅ 3 ⋅ 3 ⋅ 2 ⋅ 2) = 3 ⋅ 2 ⋅ √3 = 6√3
√48 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3) = 2 ⋅ 2 ⋅ √3 = 4√3
Then, we have
√27 + √75 + √108 - √48 = 3√3 + 5√3 + 6√3 - 4√3
√27 + √75 + √108 - √48 = 10√3
Question 3 :
Simplify the following radical expression
5√28 - √28 + 8√28
Solution :
5√28 - √28 + 8 √28
Because all the terms in the above radical expression are like terms, we can simplify as given below.
5√28 - √28 + 8√28 = 12√28
5√28 - √28 + 8√28 = 12√(2 ⋅ 2 ⋅ 7)
5√28 - √28 + 8√28 = 12 ⋅ 2√7
5√28 - √28 + 8√28 = 24√7
Question 4 :
Simplify the following radical expression
9√11 - 6√11
Solution :
9√11 - 6√11
Because the terms in the above radical expression are like terms, we can simplify as given below.
9√11 - 6√11 = 3√11
Question 5 :
Simplify the following radical expression
7√8 - 6√12 - 5√32
Solution :
7√8 - 6√12 - 5√32
Decompose 8, 12 and 32 into prime factors.
7√8 = 7√(2 ⋅ 2 ⋅ 2) = 7 ⋅ 2√2 = 14√2
6√12 = 6√(2 ⋅ 2 ⋅ 3) = 6 ⋅ 2√3 = 12√3
5√32 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2) = 5 ⋅ 2 ⋅ 2 ⋅ √2 = 20√2
Then, we have
7√8 - 6√12 + 5√32 = 14√2 - 12√3 - 20√2
7√8 - 6√12 + 5√32 = 14√2 - 12√3 - 20√2
7√8 - 6√12 + 5√32 = -6√2 - 12√3
7√8 - 6√12 + 5√32 = -6(√2 + 2√3)
Question 6 :
Simplify the following radical expression
2√99 + 2√27 - 4√176 - 3√12
Solution :
Decompose 99, 27, 176 and 12 into prime factors.
2√99 = 2√(3 ⋅ 3 ⋅ 11) = 2 ⋅ 3√11 = 6√11
2√27 = 2√(3 ⋅ 3 ⋅ 3) = 2 ⋅ 3√3 = 6√3
4√176 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 11) = 4 ⋅ 2 ⋅ 2√11 = 16√11
3√12 = 3√(2 ⋅ 2 ⋅ 3) = 3 ⋅ 2√3 = 6√3
Then, we have
2√99 + 2√27 - 4√176 - 3√12 = 6√11 + 6√3 - 16√11 - 6√3
2√99 + 2√27 - 4√176 - 3√12 = -10√11
Question 7 :
Simplify the following radical expression
3√16 - 3√2 + 43√54
Solution :
Decompose 16 and 54 into prime factors.
3√16 = √(2 ⋅ 2 ⋅ 2 ⋅ 2) = 23√2
43√54 = 43√(3 ⋅ 3 ⋅ 3 ⋅ 2) = 4(33√2) = 123√2
Then, we have
3√16 - 3√2 - 43√54 = 23√2 - 3√2 + 123√2
3√16 + 3√2 - 43√54 = 133√2
Question 8 :
Simplify the following radical expression
3√24 + 3√375 - 3√3
Solution :
Decompose 24 and 375 into prime factors.
3√24 = √(2 ⋅ 2 ⋅ 2 ⋅ 3) = 23√3
3√375 = 3√(5 ⋅ 5 ⋅ 5 ⋅ 3) = 53√3
Then, we have
3√24 + 3√375 - 3√3 = 23√3 + 53√3 - 3√3
3√24 + 3√375 - 3√3 = 63√3
Question 9 :
The orbital period of a planet is the time it takes the planet to travel around the Sun. You can fi nd the orbital period P (in Earth years) using the formula P = √d3 , where d is the average distance (in astronomical units, abbreviated AU) of the planet from the Sun.
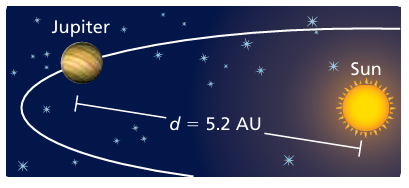
a. Simplify the formula.
b. What is Jupiter’s orbital period?
Solution :
a)
P = √d3
Simplifying the formula, we get
P = d√d
b) Applying d = 5.2
P = 5.2√5.2
= 5.2(2.28)
= 11.856
Question 10 :
The electric current I (in amperes) an appliance uses is given by the formula I = √(P/R), where P is the power (in watts) and R is the resistance (in ohms). Find the current an appliance uses when the power is 147 watts and the resistance is 5 ohms.

Solution :
I = √(P/R)
Here P = 147 watts and R = 5 ohms
I = √(147/5)
= √29.4
= 5.42
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

