SIMPLIFY RADICAL EXPRESSIONS USING THE DISTRIBUTIVE PROPERTY

The picture shown below illustrates how the distributive property can used to simplify radical expressions. 

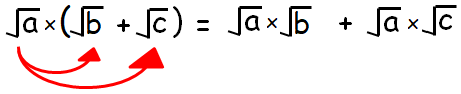
Simplifying Radicals

Example 1 : 

√a ⋅ √a  =  a

Example 2 : 

√a ⋅ √b  =  √(ab)

Example 3 :

√a / √b  =  √(a/b)

Example 4 : 

√a + √a  =  2√a

Example 5 : 

3√a - 2√a  =  √a

Question 1 :

Simplify : 

√3(√3 + √12)

Solution : 

√3(√3 + √12)  =  √3 ⋅ √3 + √3 ⋅ √12

=  3 + √(3 ⋅ 12)

=  3 + √36

=  3 + 6

=  9

Question 2 :

Simplify :  

-√2(-4 -√2)

Solution : 

-√2(-4 -√2)  =  (-√2) ⋅ (-4) + (-√2) ⋅ (-√2)

=  4√2 + 2

Question 3 :

Simplify : 

√2(7 + √5 )

Solution : 

=  √2 ⋅ 7 + √2 ⋅ √5

=  7√2 + √(2 ⋅ 5)

=  7√2 + √10

Question 4 :

Simplify : 

2(√4 + √10)

Solution : 

2(√4 + √10)  =  2 ⋅ √4 + 2 ⋅ √10

=  2 ⋅ 2 + 2 ⋅ √10

=  4 + 2√10

Question 5 :

Simplify : 

√5(√8 + √10)

Solution : 

√5(√8 + √10)  =  √5 ⋅ √8 + √5 ⋅ √10

=  √(5 ⋅ 8) + √(5 ⋅ 10)

=  √40 + √50

=  √(4 ⋅ 10) + √(25 ⋅ 2)

=  2√10 + 5√2

Question 6 :

Simplify : 

√3(√9 + √21)

Solution : 

√3(√9 + √21)  =  √3 ⋅ √9 + √3 ⋅ √21

=  √3 ⋅ 3 + √3 ⋅ √21

=  3√3 + √(3 ⋅ 21)

=  3√3 + √63

=  3√3 + √(9 ⋅ 7)

=  3√3 + 3√7

Question 7 :

Simplify : 

2√5(√6 + 2)

Solution : 

2√5(√6 + 2)  =  2√5 ⋅ √6 + 2√5 ⋅ 2

=  2√(5 ⋅ 6) + 4√5

=  2√30 + 4√5

=  2√30 + 4√5

Question 8 :

Simplify : 

√14(3 - √4)

Solution : 

√14(3 - √4)  =  √14 ⋅ 3 - √14 ⋅ √4

=  3√14 - √14 ⋅ 2

=  3√14 - 2√14

=  √14

Question 9 :

Simplify : 

√21(5 + √7)

Solution : 

√21(5 + √7)  =  √21 ⋅ 5 + √21 ⋅ √7

=  5√21 + √(21 ⋅ 7)

=  5√21 + √147

=  5√21 + √(49 ⋅ 3)

=  5√21 + 7√3

Question 10 :

Simplify : 

(5 - √3)(5 + √3)

Solution : 

Using the algebraic identity a² - b²  =  (a + b)(a - b), 

(5 - √3)(5 + √3)  =  5² - (√3)²

=  25 - 3

=  22

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.