SIMILAR TRIANGLES

Triangles which are similar will have the same shape, but not necessarily the same size.

We can use the following postulates and theorem to check whether two triangles are similar or not.

Triangle Similarity Postulates and Theorems

1. Angle-Angle (AA) Similarity Postulate :

If two angles of one triangle are congruent to two angles of another, then the triangles must be similar.

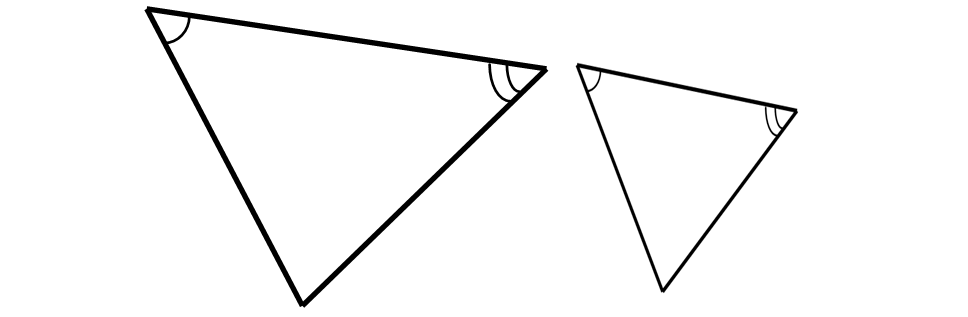
2. Side-Side-Side (SSS) Similarity Theorem :

If the lengths of the corresponding sides of two triangles are proportional, then the triangles must be similar.

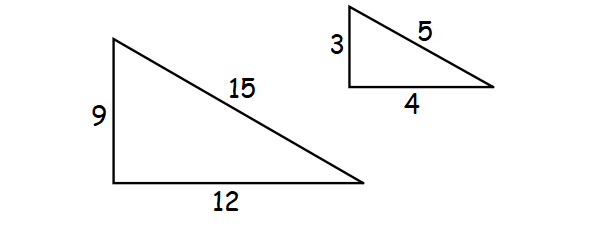
3. Side-Angle-Side (SAS) Similarity Theorem :

If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the sides including these angles are proportional, then the triangles must be similar.

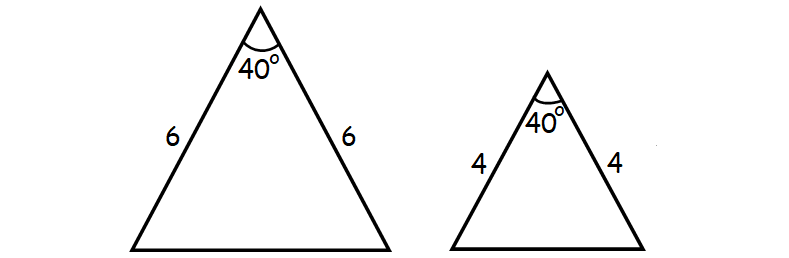
Solved Problems

Problem 1 :

Determine whether the two triangles given below are similar. Justify your answer.

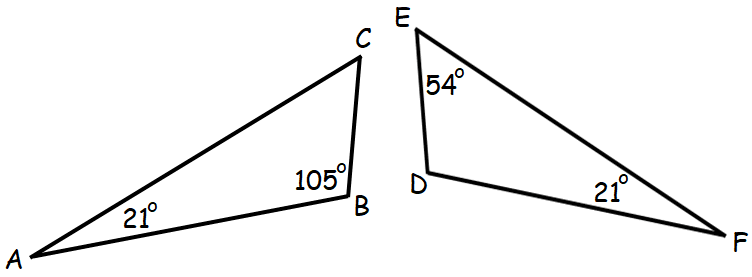
Solution :

By Triangle Sum Theorem, in Δ ABC,

∠A + ∠B + ∠C = 180°

21° + 105° + ∠C = 180°

126° + ∠C = 180°

Subtract 126° from both sides.

∠C = 54°

In triangles ABC and DEF, we have

∠A = ∠F = 21°

∠E = ∠C = 54°

Two angles of one triangle are congruent to two angles of another triangle.

By Third Angle Theorem, the third pair of angles must also be congruent.

∠B = ∠D = 105°

So, the triangles ABC and DEF are similar triangles.

Problem 2 :

Determine whether the two triangles given below are similar. Justify your answer.

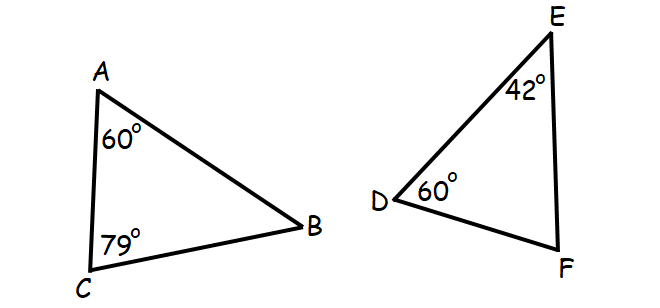
Solution :

By Triangle Sum Theorem, in Δ ABC,

∠A + ∠B + ∠C = 180°

60° + ∠B + 79° = 180°

∠B + 139° = 180°

Subtract 139° from both sides.

∠B = 41°

By Triangle Sum Theorem, in Δ DEF,

∠D + ∠E + ∠F = 180°

60° + 42° + ∠F = 180°

102° + ∠F = 180°

Subtract 102° from both sides.

∠F = 78°

In triangles ABC and DEF, we have

∠A = ∠D = 60°

And no more pairs of angles are not congruent.

So, the triangles ABC and DEF are not similar triangles.

Problem 3 :

For what value of x, is triangle ABC similar to triangle DEF ?

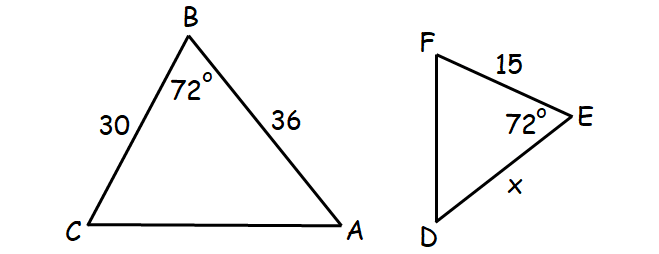
Solution :

Let us assume the given two triangles are similar.

So, the ratio of the corresponding sides must be equal.

By taking the vertices of the triangle in the order (given) ABC and DEF, we have

AB/DE = BC/EF

36/x = 30/15

Take reciprocal on both sides.

x/36 = 15/30

x/36 = 1/2

Multiply both sides by 36.

x = 1/2 ⋅ 36

x = 18

So, the two triangles ABC and DEF are similar for the value of x is 18.

Problem 4 :

Find the value of h in the diagram given below.

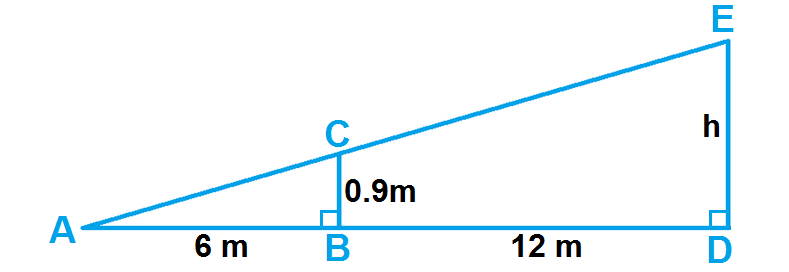
Solution :

In the above diagram, we can consider two triangles ABC and ADE.

In triangles ABC and ADE, we have

∠B and ∠D are right angles

∠A is common angle

Two angles of one triangle are congruent to two angles of another triangle.

By Third Angle Theorem, the third pair of angles must also be congruent.

So, the triangles ABC and ADE are similar triangles.

In similar triangles, the ratio of the corresponding sides are equal.

Then, we have

AB/AD = BC/DE ----(1)

Find the length of AD :

AD = AB + BD

AD = 6 + 12

AD = 18

Substitute AB = 6, AD = 18, BC = 0.9 and DE = h in (1).

6/18 = 0.9/h

Take reciprocal on both sides.

18/6 = h/0.9

3 = h/0.9

Multiply both sides by 0.9.

2.7 = h

Problem 5 :

In the diagram given below, if AC and DE are parallel, find the value of h.

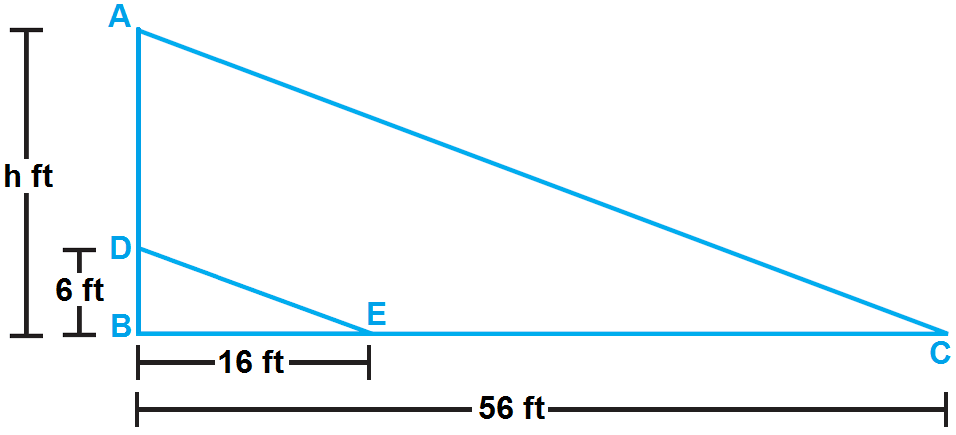
Solution :

In the above diagram, we can consider two triangles ABC and DBE.

Given : AC and DE are parallel.

The parallel sides AC and DE are cut by the transversal EC.

Then ∠E and ∠C are corresponding angles.

When two parallel lines cut by a transversal, the corresponding angles are congruent.

So, ∠E and ∠C are congruent.

In triangles ABC and DBE, we have

∠E ≅ ∠C

∠B is common angle

Two angles of one triangle are congruent to two angles of another triangle.

By Third Angle Theorem, the third pair of angles must also be congruent.

So, the triangles ABC and DBE are similar triangles.

In similar triangles, the ratio of the corresponding sides are equal.

AB/DB = BC/BE

Substitute AB = h, DB = 6, BE = 16 and BC = 56.

h/6 = 56/16

Multiply both sides by 6.

h = (56/16) ⋅ 6

 h = 21

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.