SIMILAR TRIANGLES AND PROPORTIONAL PARTS

Triangles which are similar will have the same shape, but not necessarily the same size.

We can use the following postulates and theorem to check whether two triangles are similar or not.

Angle-Angle (AA) Similarity Postulate :

If two angles of one triangle are congruent to two angles of another, then the triangles must be similar.

Proportional Parts

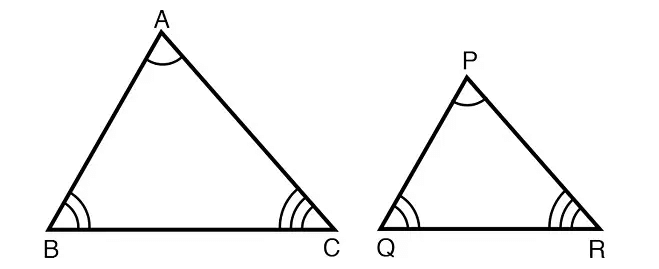
In the triangles shown above,

∠A ≅ ∠P

∠B ≅ ∠Q

∠C ≅ ∠R

So, two triangles ABC and PQR shown above are similar.

ΔABC ∼ ΔPQR

Three pairs of corresponding sides :

(AB, PQ), (BC, QR) and (CA, RQ)

If two triangles are similar, the corresponding sides are proportional.

Solved Problems

Problem 1 :

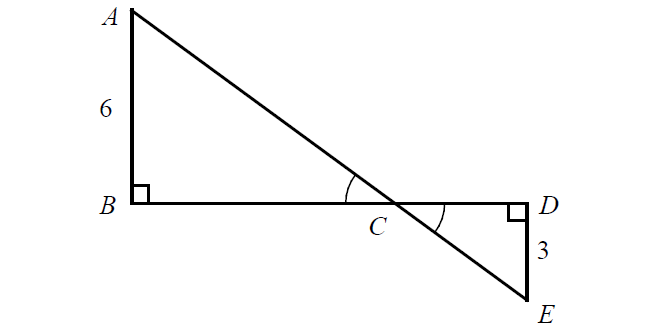
In the figure above, if AB = 6, DE = 3, and BD = 12, what is the length of BC?

Solution :

Given : BD = 12.

Let BC = x. Then DC = 12 - x.

In the figure above,

∠B ≅ ∠D

∠ACB ≅ ∠DCE

By Angle-Angle (AA) Similarity Postulate,

ΔABC ∼ ΔEDC

6(12 - x) = 3x

72 - 6x = 3x

72 = 9x

8 = x

BC = 8

Problem 2 :

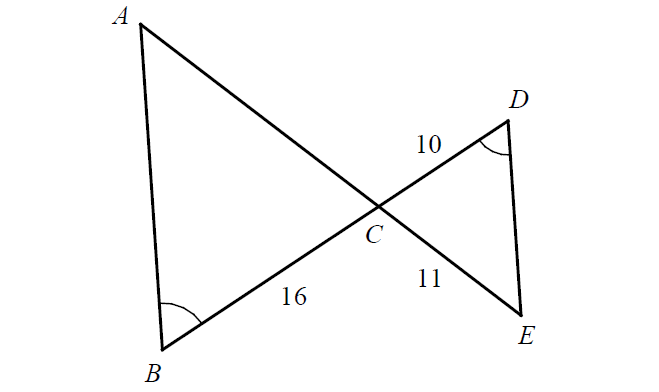
In the figure above, ∠B ≅ ∠D.

If BC = 16, CD = 10, and CE = 11, what is the length of AE?

Solution :

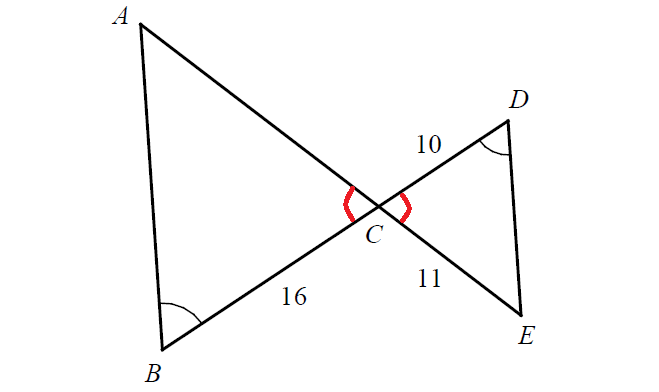
In the triangle above, the two angles marked in red color are vertically opposite angles and they are congruent.

Let AC = x.

In the figure above,

∠B ≅ ∠D

∠ACB ≅ ∠DCE

By Angle-Angle (AA) Similarity Postulate,

ΔABC ∼ ΔEDC

5x = 88

x = 17.6

AC = 17.6

AE = AC + CE

AE = 17.6 + 11

AE = 27.6

Problem 3 :

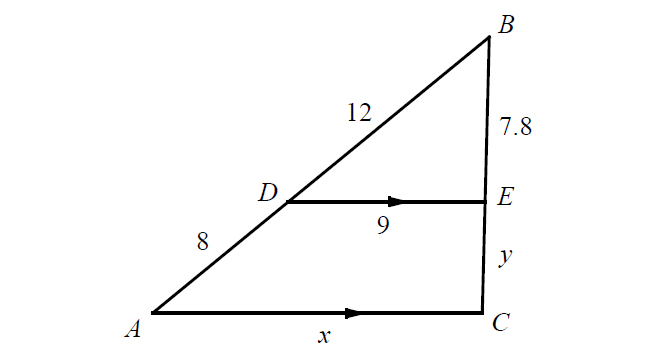
In the figure above, if DE||AC, find the values of x and y.

Solution :

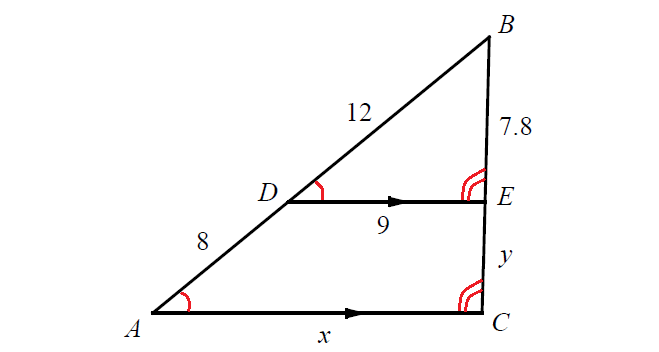
Since DE||AC, the corresponding angles are congruent. In the figure above, ∠A & ∠D are corresponding angles and they are congruent and ∠C & ∠E are corresponding angles and they are congruent.

In the figure above,

∠A ≅ ∠D

∠C ≅ ∠E

By Angle-Angle (AA) Similarity Postulate,

ΔABC ∼ ΔDBE

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.