SIMILAR SOLIDS

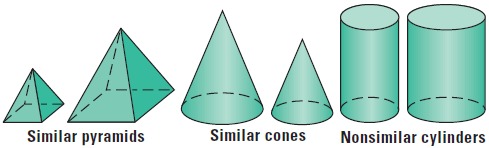
Two solids with equal ratios of corresponding linear measures, such as heights or radii, are called similar solids.

This common ratio is called the scale factor of one solid to the other solid. Any two cubes are similar ; so are any two spheres. 

Here are other examples of similar and non-similar solids.

Similar Solids Theorem

Theorem :

If two similar solids have a scale factor of a : b, then corresponding areas have a ratio of

a² : b²

and corresponding volumes have a ratio of

a³ : b³

The term areas in the theorem above can refer to any pair of corresponding areas in the similar solids, such as lateral areas, base areas, and surface areas.

Identifying Similar Solids - Examples

Example 1 :

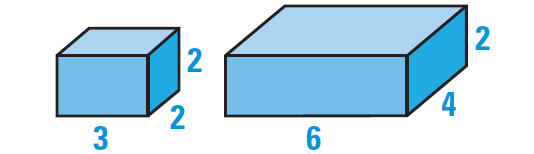
Decide whether the two solids are similar. If so, compare the surface areas and volumes of the solids.

Solution :

Find the ratios of corresponding linear measures as shown below.

Lengths  :  3/6  =  1/2

Widths  :  2/4  =  1/2

Heights  :  2/2  =  1/1

Because the ratios of corresponding linear measures are not equal, the solids are not similar.

Example 2 :

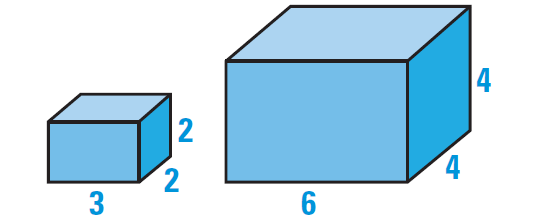
Decide whether the two solids are similar. If so, compare the surface areas and volumes of the solids.

Solution :

Find the ratios of corresponding linear measures as shown below.

Lengths  :  3/6  =  1/2

Widths  :  2/4  =  1/2

Heights  :  2/4  =  1/2

Because the ratios of corresponding linear measures are equal, the solids are similar. 

The surface area and volume of the solids are as follows :

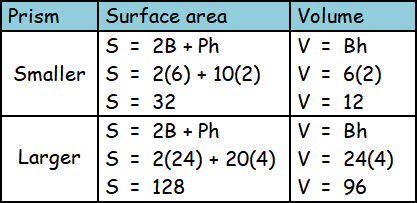
The ratio of side lengths is

=  1 : 2

The ratio of surface  areas is

=  32 : 128

=  1 : 4

The ratio of volumes is

=  12 : 96

=  1 : 8

Finding the Scale Factor of Similar Solids 

Example 3 :

Find the scale factor of the two cubes shown below. 

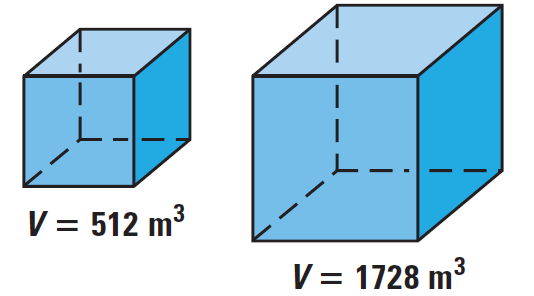
Solution :

To find the scale factor of the two cubes, find the ratio of the two volumes.

Write ratio of volumes. 

a³ : b³  =  512 : 1728

Use a calculator to take the cube root.

a : b  =  8 : 12

Simplify. 

a : b  =  2 : 3

So, the two cubes have a scale factor of 2 : 3.

Using the Scale Factor of Similar Solids

Example 4 :

The prisms shown below are similar with a scale factor of 1:3. Find the surface area and volume of prism G given that the surface area of prism F is 24 square feet and the volume of prism F is 7 cubic feet.

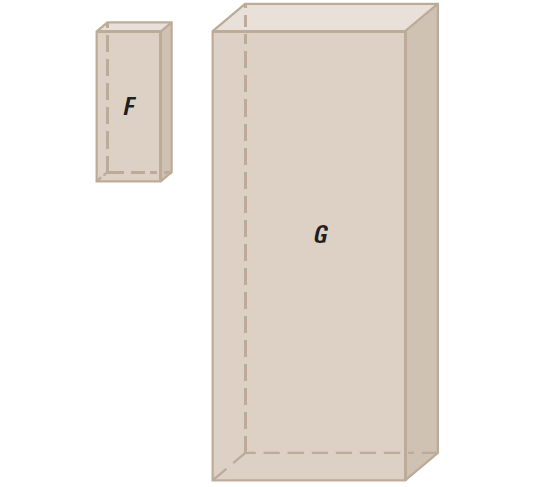
Solution :

Use Similar Solids Theorem to set up two proportion. 

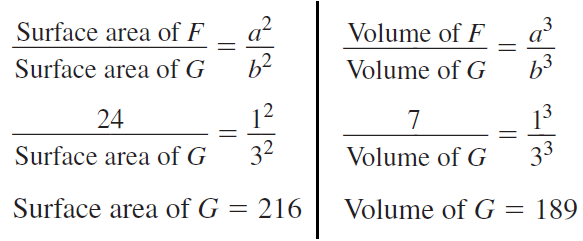
So, the surface area of prism G is 216 square feet and the volume of prism G is 189 cubic feet.

Using Volumes of Similar Solids

Example 5 :

The lift power of a weather balloon is the amount of weight the balloon can lift. Find the missing measures in the table below, given that the ratio of the lift powers is equal to the ratio of the volumes of the balloons.

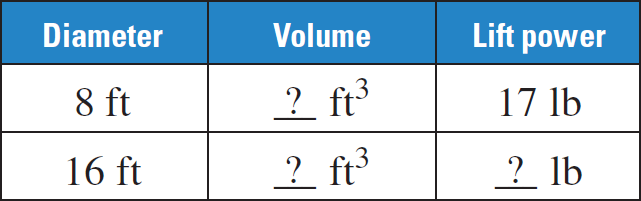
Solution :

Find the volume of the smaller balloon, whose radius is 4 feet.

Smaller Balloon : 

V  =  4/3 ⋅ πr³

Substitute 4 for r. 

V  =  4/3 ⋅ π(4³)

Simplify. 

V  =  256π / 3

Use calculator. 

V  ≈  85.3π  ft³

The scale factor of the two balloons is

=  8 : 16

=  1 : 2

So, the ratio of the volumes is

=  1³ : 2³

=  1 : 8

To find the volume of the larger balloon, multiply the volume of the smaller balloon by 8.

Larger Balloon :

V  ≈  8(85.3π)

V  ≈  682.4π  ft³

The ratio of the lift powers is 1 : 8. To find the lift power of the larger balloon, multiply the lift power of the smaller balloon by 8, as follows :

8(17)  =  136 lb

Comparing Similar Solids

Example 6 :

Two swimming pools are similar with a scale factor of 3 : 4. The amount of a chlorine mixture to be added is  proportional to the volume of water in the pool. If two cups of the chlorine mixture are needed for the smaller pool, how much of the chlorine mixture is needed for the larger pool ?

Solution :

Using the scale factor, the ratio of the volume of the smaller pool to the volume of the larger pool is as follows :

a³ : b³  =  3³ : 4³

a³ : b³  =  27 : 64

a³ : b³  ≈  1 : 2.4

The ratio of the volumes of the mixtures is 1 : 2.4. The amount of the chlorine mixture for the larger pool can be found by multiplying the amount of the chlorine mixture for the smaller pool by 2.4 as follows :

2(2.4)  =  4.8 c

So, the larger pool needs 4.8 cups of the chlorine mixture.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.