SIMILAR FIGURES

Two figures are similar if one can be obtained from the other by a sequence of translations, reflections, rotations, and dilations. Similar figures have the same shape but they may have different sizes.

If two figures are similar, there must be a sequence of translations, reflections, rotations, and/or dilations that can transform one to the other.

Example 1 :

Identify a sequence of transformations that can transform figure A into figure B. Say whether the figures are congruent. And also, say whether they are similar.

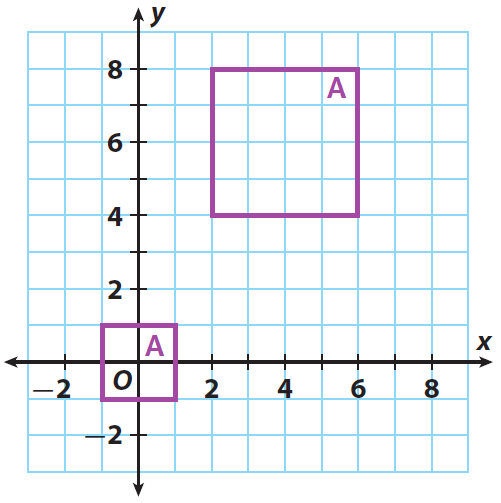
Solution : 

Step 1 : 

Both figures are squares whose orientations are the same, so no reflection or rotation is needed.

Step 2 : 

Figure B has sides twice as long as figure A, so a dilation with a scale factor of 2 is needed.

Step 3 :

Figure B is moved to the right and above figure A, so a translation is needed.

Step 4 : 

A sequence of transformations that will accomplish this is a dilation by a scale factor of 2 centered at the origin followed by the translation

(x, y) ----> (x + 4, y + 6)

The figures are not congruent, but they are similar.

Example 2 :

Identify a sequence of transformations that can transform figure X into figure Y. Include a reflection. Say whether the figures are congruent. And also, say whether they are similar.

Solution : 

Step 1 : 

The orientation of figure Y is reversed from that of figure X, so a reflection over the y-axis is needed.

Step 2 : 

Figure Y has sides that are half as long as figure X, so a dilation with a scale factor of 1/2 is needed.

Step 3 :

Figure B is moved to the right and above figure A, so a translation is needed.

Step 4 : 

Figure Y is moved above figure X, so a translation is needed.

Step 5 : 

A sequence of transformations that can accomplish this is a dilation by a scale factor of 1/2 centered at the origin, followed by the reflection

(x, y) ---> (-x , y)

followed by the translation

(x, y) ---> (x , y + 5)

The figures are not congruent, but they are similar.

Example 3 :

In example 2, identify a sequence of transformations that can transform figure X into figure Y. Include a rotation.

Solution : 

Step 1 : 

The orientation of figure Y is reversed from that of figure X, so a rotation of 180º is needed.

Step 2 : 

Figure Y has sides that are half as long as figure X, so a dilation with a scale factor of 1/2 is needed.

Step 3 :

Figure Y is moved above figure X, so a translation is needed.

Step 4 : 

Figure Y is moved above figure X, so a translation is needed.

Step 5 : 

A sequence of transformations that can accomplish, this is a rotation of 180º about the origin, followed by a dilation by a scale factor of 1/2 centered at the origin, followed by the translation

(x, y) ---> (x , y + 5)

The figures are not congruent, but they are similar.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.