SIDE ANGLE SIDE Congruence Postulate

Side-Angle-Side or SAS Congruence Postulate is a rule which can be used to prove the congruence of two triangles.

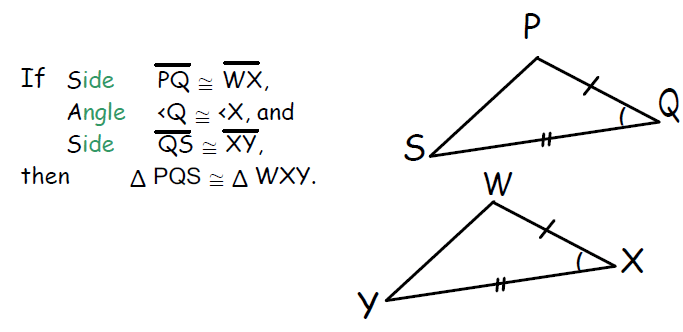
Explanation :

If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent.

Solved Examples

Example 1 :

In the diagram given below, prove that ΔAEB ≅ ΔDEC using two column proof.

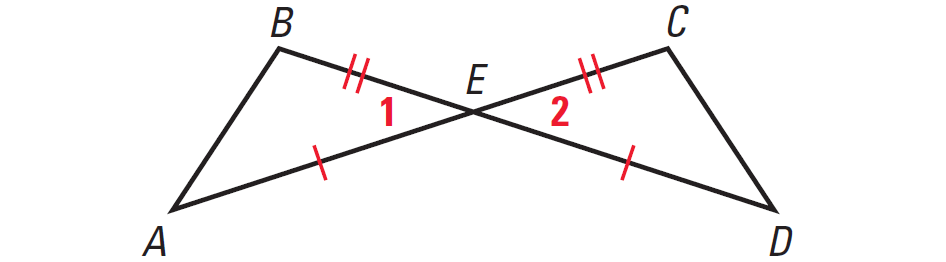
Solution :

Example 2 :

Check whether two triangles PQR and JKL are congruent. 

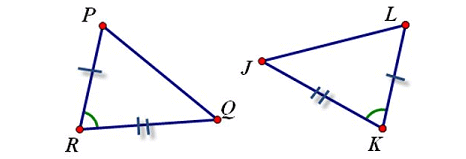
Solution :

(i) PR  =  LA (Given)

(ii) ∠R  =  ∠K (Given)

(i) RQ  =  JK (Given)

Hence, the two triangles PQR and JKL are congruent by SAS postulate.

Other Triangle Congruence Postulates and Theorems

1. Side-Side-Side (SSS) Congruence Postulate

If three sides of one triangle is congruent to three sides of another triangle, then the two triangles are congruent.

2. Angle-Side-Angle (ASA) Congruence Postulate

If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.

3. Angle-Angle-Side (AAS) Congruence Postulate

If two angles and non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent.

4. Hypotenuse-Leg (HL) Theorem

If the hypotenuse and one leg of a right triangle are equal to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent.

5. Leg-Acute (LA) Angle Theorem

If a leg and an acute angle of one right triangle are congruent to the corresponding parts of another right triangle, then the two right triangles are congruent.

6. Hypotenuse-Acute (HA) Angle Theorem

If the hypotenuse and an acute angle of a right triangle are congruent to the hypotenuse and an acute angle of another right triangle, then the two triangles are congruent.

7. Leg-Leg (LL) Theorem

If the legs of one right triangle are congruent to the legs of another right triangle, then the two right triangles are congruent.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.