SHIFTING THE GRAPH RIGHT OR LEFT EXAMPLES

The procedure for shifting the graph of a function to the right is illustrated by the following example:

Question 1 :

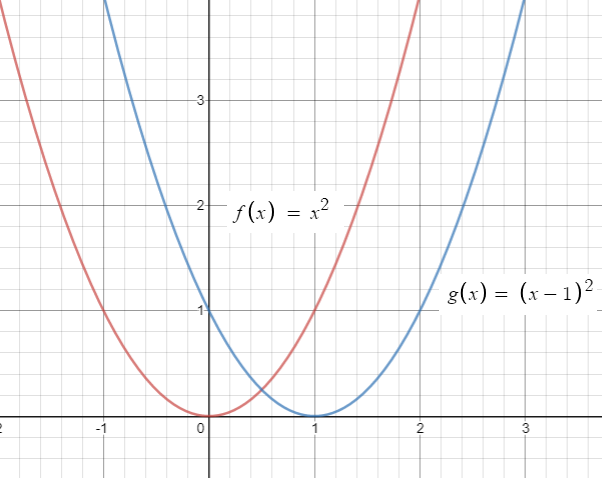
Define a function g by g(x) = f(x − 1), where f is the function defined by f(x) = x², with the domain of f the interval [−1, 1].

(a) Find the domain of g.

(b) Find the range of g.

(c) Sketch the graph of g.

Solution :

(a) Here the function g(x) is defined precisely when f(x − 1) is defined. The domain of the function f(x) is [-1, 1]. By adding 1 with coordinates, we will get domain of g(x).

[-1+1, 1+1]  ==>  [0, 2]

(b) The range of f is [0, 1], we see that the values taken on by g are the same as the values taken on by f . Thus the range of g equals the range of f , which is the interval [0, 1].

(c)  Sketch the graph of g(x)  =  (x - 1)²

Since 1 is subtracted from x, we have to move the graph 1 unit to the right side.

Question 2 :

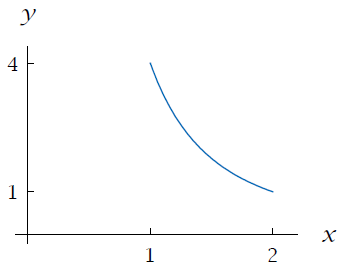
Assume that f is the function defined on the interval [1, 2] by the formula f(x) = 4 / x² . Thus the domain of f is the interval [1, 2], the range of f is the interval [1, 4], and the graph of f is shown here.

The graph of g is obtained by shifting the graph of f left 3 units 

For each function g described below:

(a) Sketch the graph of g.

(b) Find the domain of g (the endpoints of this interval should be shown on the horizontal axis of your sketch of the graph of g).

(c) Give a formula for g.

(d) Find the range of g (the endpoints of this interval should be shown on the vertical axis of your sketch of the graph of g).

Solution :

Shifting the graph of f left 3 units gives this graph.

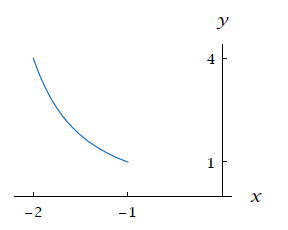
(b)  The domain of g is obtained by subtracting 3 from every number in domain of f . Thus the domain of g is the interval [−2,−1].

(c)  Because the graph of g is obtained by shifting the graph of f left 3 units, we have g(x) = f(x + 3). Thus g(x) = 4/(x + 3)² for each number x in the interval [−2,−1].

(d) The range of g is the same as the range of f. Thus the range of g is the interval [1, 4].

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.