SET THEORY WORKSHEET

Question 1 : 

Which of the following are sets ? 

(i)  The collection of good books.

(ii)  The collection of prime numbers less than 30.

(iii) The collection of ten most talented mathematics teachers.

(iv)  The collection of all students in your school.

(v)  The collection of all even numbers.

Question 2 :

Let A = {0, 1, 2, 3, 4, 5}. Insert the appropriate symbol ∈ or ∉ in the blank spaces.

(i) 0 ___ A

(ii) 6 ___ A

(iii) 3 ___ A

(iv) 4 ___ A

(v) 7 ___ A

Question 3 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 5, 6, 7}, find A u B. 

Question 4 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 5, 6, 7}, find A n B. 

Question 5 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 7}, Check whether A and B are disjoint sets. 

Question 6 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 5, 6, 7}, find A\ B. 

Question 7 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 5, 6, 7}, find A Δ  B. 

Question 8 : 

Let U  =  {1, 2, 3, 4, ......10}, A  =  {5, 6, 7, 9}, find A'. 

Question 9 :

Write the following set in set-builder form. 

The set of odd numbers between 0 and 10

Question 10 :

Write the following set in Roster form.

{x : x is an integer, x² ≤ 16}

Question 11 :

Write the following set in descriptive form.

S  =  {3, 6, 9, 12, ...................} 

Question 12 :

Let A  =  {1, 2, 3, 4, 5} and B  =  { 5, 3, 4, 2, 1}. Determine whether B is a proper subset of A. 

Question 13 :

Let A  =  {1, 2, 3, 4, 5} and B  =  {1, 2, 5}. Determine whether B is a proper subset of A. 

Question 14 :

Let A  =  {a, e, i, o, u} find the number of proper subsets of A. 

Question 15 :

Let A  =  {a, b, c} find the power set of A.

Question 16 :

Let A  =  {1, 3, 5, 7} find the cardinality of power set of A.

Question 17 :

In a class of 50 students, each of the students passed either in mathematics or in science or in both. 10 students passed in both and 28 passed in science. Find how many students passed in mathematics ?

Question 18 :

In a group of students, 65 play foot ball, 45 play hockey, 42 play cricket, 20 play foot ball and hockey, 25 play foot ball and cricket, 15 play hockey and cricket and 8 play all the three games. Find the total number of students in the group (Assume that each student in the group plays at least one game).

Question 19 :

In a class of 60 students, 40 students like math, 36 like science, 24 like both the subjects. Find the number of students who like

(i) Math only, (ii) Science only  (iii) Either Math or Science (iv) Neither Math nor science.

Question 20 :

At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. Find the number of women doctors attending the conference.

Detailed Answer Key

Question 1 : 

Which of the following are sets ? 

(i)  The collection of good books.

(ii)  The collection of prime numbers less than 30.

(iii) The collection of ten most talented mathematics teachers.

(iv)  The collection of all students in your school.

(v)  The collection of all even numbers.

Answer :

(i)  Not a set

(ii)  Set

(iii)  Not a set

(iv)  Set

(v)  Set

Question 2 :

Let A = {0, 1, 2, 3, 4, 5}. Insert the appropriate symbol ∈ or ∉ in the blank spaces.

(i) 0 ___ A

(ii) 6 ___ A

(iii) 3 ___ A

(iv) 4 ___ A

(v) 7 ___ A

Answer :

(i)  0 ∈ A

(ii)  6 ∉ A

(iii)  3 ∈ A

(iv)  4 ∈ A

(v)   7 ∉ A

Question 3 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 5, 6, 7}, find A u B. 

Answer :

A u B  =  {1, 3, 5, 6} u {0, 5, 6, 7}

A u B  =  {0, 1, 3, 5, 6, 7}

Question 4 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 5, 6, 7}, find A n B. 

Answer :

A n B  =  {1, 3, 5, 6} u {0, 5, 6, 7}

A u B  =  {5, 6}

Question 5 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 7}, Check whether A and B are disjoint sets. 

Solution :

A n B  =  {1, 3, 5, 6} u {0, 7}

A u B  =  {   }  or  Empty set

Hence, A and B are disjoint sets.

Question 6 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 5, 6, 7}, find A\ B. 

Solution :

A \ B  =  {1, 3, 5, 6} \ {0, 5, 6, 7}

A \ B  =  {1, 3}

Question 7 : 

Let A  =  {1, 3, 5, 6}, B  =  {0, 5, 6, 7}, find A Δ  B. 

Answer :

A \ B  =  {1, 3, 5, 6} \  {0, 5, 6, 7}  =  {1, 3}

B \ A  =  {0, 5, 6, 7} \ {1, 3, 5, 6}  =  {0, 7}

A Δ B  =  (A \ B) u (B \ A)

A Δ B  =  {1, 3} u {0, 7}

A Δ B  =  {1, 3, 0, 7}

Question 8 : 

Let U  =  {1, 2, 3, 4, ......10}, A  =  {5, 6, 7, 9}, find A'. 

Answer :

A'  =  U \ A

A'  =  {1, 2, 3, 4, ......10} \ {5, 6, 7, 9}

A'  =  {1, 2, 3, 4, 8, 10}

Question 9 :

Write the following set in set-builder form. 

The set of odd numbers between 0 and 10

Answer : 

{2x - 1 : x is an integer in the interval 0 < x < 5}

Question 10 :

Write the following set in Roster form.

{x : x is an integer, x² ≤ 16}

Answer : 

 {-4, -3, -2, -1, 0, 1, 2, 3, 4}

Question 11 :

Write the following set in descriptive form.

S  =  {3, 6, 9, 12, ...................} 

Answer :

The given set contains multiples of 3. So, we can represent the above set in descriptive form as follows.

S is the multiples of 3

Question 12 :

Let A  =  {1, 2, 3, 4, 5} and B  =  { 5, 3, 4, 2, 1}. Determine whether B is a proper subset of A. 

Answer : 

If B is the proper subset of A, every element of B must also be an element of A and also B must not be equal to A. 

In the given sets A and B, every element of B is also an element of A. But B is equal A.

So, B is the subset of A, but not a proper subset. 

Question 13 :

Let A  =  {1, 2, 3, 4, 5} and B  =  {1, 2, 5}. Determine whether B is a proper subset of A. 

Answer : 

If B is the proper subset of A, every element of B must also be an element of A and also B must not be equal to A. 

In the given sets A and B, every element of B is also an element of A.

And also But B is not equal to A.

So, B is a proper subset of A. 

Question 14 :

Let A  =  {a, e, i, o, u} find the number of proper subsets of A. 

Answer : 

Let the given set contains n number of elements.

Then, the formula to find number of proper subsets is

=  2^n-1

The value of n for the given set A is 5.

Because the set A =  {a, e, i, o, u} contains 5 elements. 

Number of proper subsets  =  2^5-1

=  2⁴

=  16

So, the number of proper subsets of A is 16.

Question 15 :

Let A  =  {a, b, c} find the power set of A.

Answer : 

We know that the power set is the set of all subsets.

Here, the given set A contains 3 elements.

Then, the number of subsets  =  2³ =  8.

Therefore, 

P(A)  =  {{a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}, { }}

Question 16 :

Let A  =  {1, 3, 5, 7} find the cardinality of power set of A.

Answer : 

The formula for cardinality of power set of A is given below. 

n[P(A)]  =  2ⁿ

Here n stands for the number of elements contained by the given set A. 

The given set A contains 4 elements. So, n = 4. 

Then, we have 

n[P(A)]  =  2⁴

n[P(A)]  =  16

So, the cardinality of the power set of A is 16.

Question 17 :

In a class of 50 students, each of the students passed either in mathematics or in science or in both. 10 students passed in both and 28 passed in science. Find how many students passed in mathematics?

Solution :

Let M = The set of students passed in Mathematics

S = The set of students passed in Science

Then,

total number of students  n (M U S)  =  50

Number of students passed in both subjects n(MnS) = 10

Number of students passed in science n (S)  =  28

From this, we have to find the number of students who passed in mathematics.

n (M U S)  = n (M) + n (S) -  n (M n S)

50  =  n (M) + 28 - 10

50  =  n (M) + 18

Subtract 18 on both sides

50 - 18 = n (M) + 18 - 18

n (M) = 32

So, the number students passed in Mathematics is 32.

Question 18 :

In a group of students, 65 play foot ball, 45 play hockey, 42 play cricket, 20 play foot ball and hockey, 25 play foot ball and cricket, 15 play hockey and cricket and 8 play all the three games. Find the total number of students in the group (Assume that each student in the group plays at least one game).

Answer :

Venn diagram related to the information given in the question :

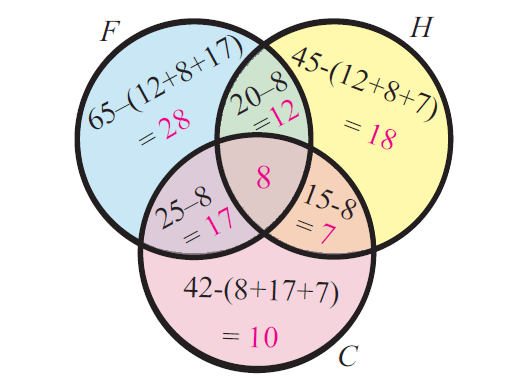
Total number of students in the group :

=  28 + 12 + 18 + 7 + 10 + 17 + 8

=  100

So, the total number of students in the group is 100.

Question 19 :

In a class of 60 students, 40 students like math, 36 like science, 24 like both the subjects. Find the number of students who like

(i) Math only, (ii) Science only  (iii) Either Math or Science (iv) Neither Math nor science.

Answer :

Step 1 :

Let M and S represent the set of students who like math and science respectively.

Step 2 :

From the information given in the question, we have

n(M)  =  40, n(S)  =  36, n(MnS)  =  24

Step 3 :

Answer (i) :

No. of students who like math only :

=  n(M) - n(MnS)

=  40 - 24

=  16

Step 4 :

Answer (ii) :

No. of students who like science only :

=  n(S) - n(MnS)

=  36 - 24

=  12

Step 5 :

Answer (iii) :

No. of students who like either math or science :

=  n(M or S) 

=  n(MuS) 

=  n(M) + n(S) - n(MnS)

=  40 + 36 - 24

=  52

Step 6 :

Answer (iv) :

Total no. students who like Maths or Science subjects :

n(MuS)  =  52

No. of students who like neither math nor science

=  60 - 52

=  8

Question 20 :

At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. Find the number of women doctors attending the conference.

Answer :

Step 1 :

Let M and D represent the set of Indian men and Doctors respectively.

Step 2 :

From the information given in the question, we have

n(M)  =  23, n(D)  =  4, n(MuD)  =  24 

Step 3 :

From the basic stuff, we have

n(MuD)  =  n(M) + n(D) - n(MnD)

24  =  23 + 4 - n(MnD)

n(MnD)  =  3 

n(Indian Men and Doctors)  =  3

Step 4 :

So, out of the 4 Indian doctors,  there are 3 men.

And the remaining 1 is Indian women doctor.

So, the number women doctors attending the conference is 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.