SEGMENTS AND THEIR MEASURES WORKSHEET

Problem 1 :

Measure the length of the segment to the nearest millimeter.

Problem 2 :

Use the map to find the distances between the three cities that lie on a line.

1. Answer :

Use a metric ruler.

Align one mark of the ruler with A, then estimate the coordinate of B.

For example, if we align A with 3, B appears to align with 5.5 as shown below.

Now, we have

AB  =  |5.5 - 3|  =  |2.5|  =  2.5

The distance between A and B is 2.5 cm.

Note :

It does not matter, how we place the ruler.

For example, if the ruler in the above example is placed such that A is aligned with 4, then B aligns with 6.5. The difference in the coordinates is same.

That is,

AB  =  |6.5 - 4|  =  |2.5|  =  2.5

2. Answer :

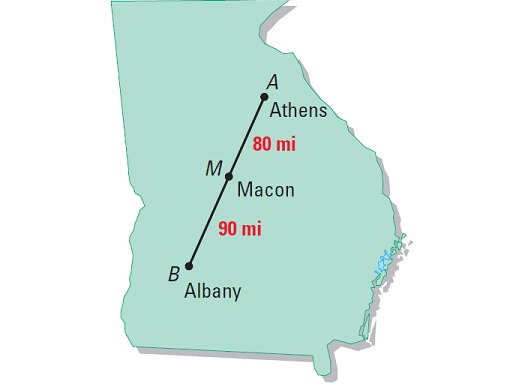
Using the scale on the map, we can estimate that the difference between Athens and Macon is

AM  =  80 miles

The distance between Macon and Albany is

MB  =  90 miles

It has been explained in the picture given below.

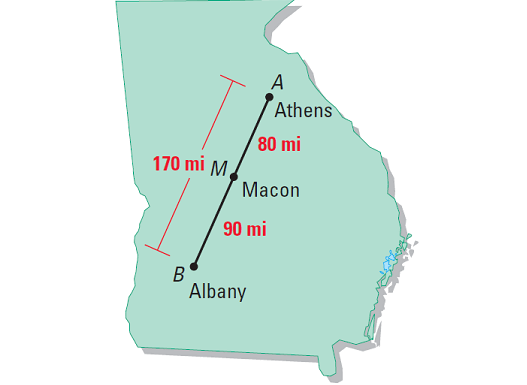
Knowing that Athens, Macon and Albany lie on the same line, we can use the Segment Addition Postulate to conclude that the distance between Athens and Albany is 

AB  =  AM + MB

AB  =  80 + 90

AB  =  170 miles

It has been explained in the picture given below.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.