SCATTER PLOTS AND ASSOCIATION

We know that a set of bivariate data involves two variables. Bivariate data can be used to explore the relationship between two variables. We can graph bivariate data on a scatter plot. A scatter plot is a graph with points plotted to show the association between two variables or two sets of data.

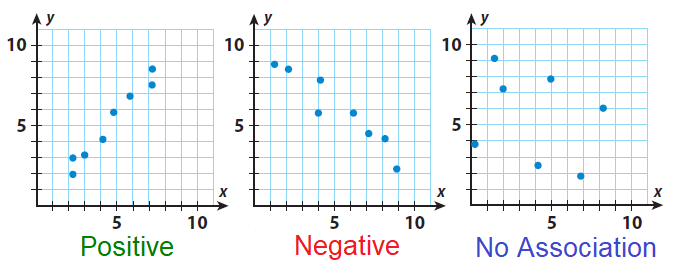
Data that show a positive or negative association and lie basically along a line exhibit a linear association. Data that show a positive or negative association but do not lie basically along a line exhibit a nonlinear association.

Example 1 :

The final question on a science test reads, how many hours spent studying for this test. The teacher records the number of hours each student studied and the marks scored by the respective student on the test.

Describe the type of association between number of hours spent for studying and marks scored using scatter plot. 

Solution :

Step 1 :

Make a prediction about the relationship between the number of hours spent studying and marks scored.

When we look at the above data, we can make the following prediction. A greater number of study hours are likely to be associated with higher marks.

Step 2 :

Make a scatter plot. Graph hours spent studying as the independent variable and marks scored by the students as the dependent variable.

Moreover, if we consider hours spent for studying as variable "x" and marks scored by the students as variable "y", we can write the above data as ordered pairs in the form (x, y).

Then, we have

       (0, 75), (0.5, 80), (1, 80), (1, 85), (1.5, 85), (1.5, 95),                            (2, 90), (3, 100) and (4, 90). 

Plot these points on a graph paper. 

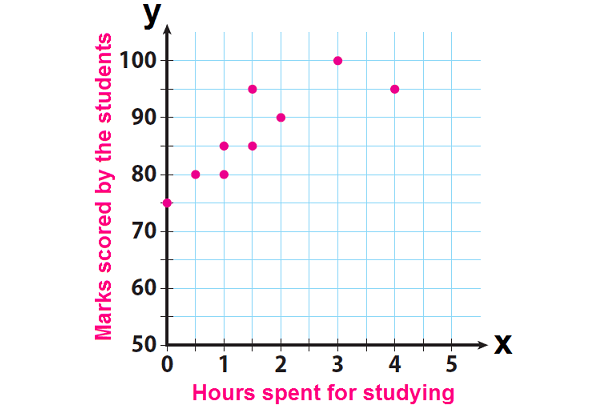
The graph shows a general upward trend. So the association between number of hours spent for studying and marks scored is positive. That is, as number of hours is getting increased, the marks scored is also getting increased. 

Example 2 :

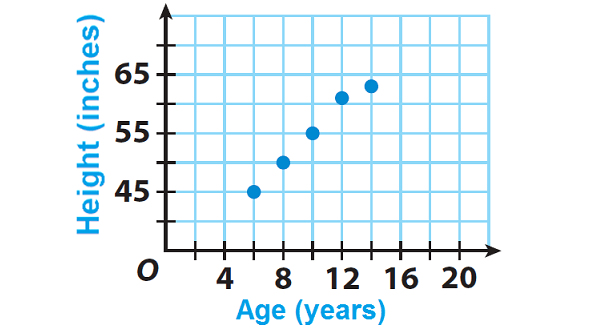
The scatter plot shows David’s height at various ages. Describe the type of association between David’s age and his height. Explain.

Solution :

As David is getting older, his height increases roughly along a straight line on the graph, so the association is positive and basically linear.

Example 3 :

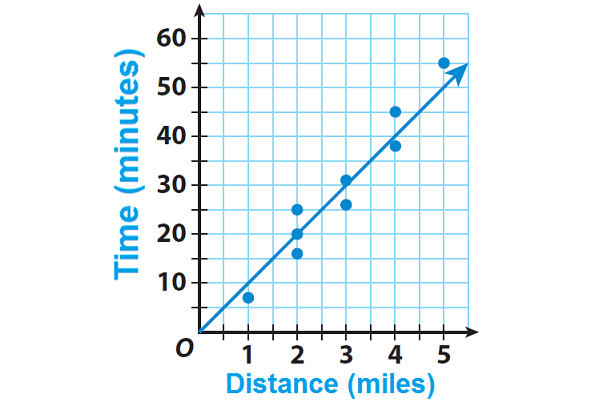
Alexa is training for a 10K race. For each of her training runs, she recorded the distance she ran and the time she ran. She made a scatter plot of her data and drew a trend line. Use the trend line to predict how long it would take Alexa to run 4.5 miles.

Solution :

For a distance of 4.5 miles, the trend line shows a time of 45 minutes. So, it will take Alexa about 45 minutes to run 4.5 miles.

Example 4 :

David asked 20 people if they can buy a new product that he developed at each of several prices. The scatter plot shows how many of the 20 people said “yes” at a given price. Describe the association between price and the number of buyers.

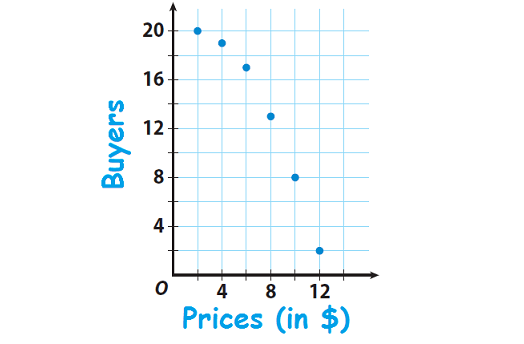
Solution :

When price gets increased, the number of buyers gets  decreased. So, there is a negative association. Because the data points do not lie along a line, the association is non-linear.

Example 5 :

A survey made among students in a district and the scatter plot shows the level of reading and height for 16 students in the district. Describe the association and give a possible reason for it.

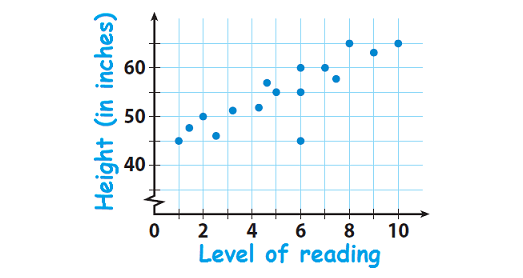
Solution :

Positive and basically linear :

The students who are taller read at a higher level.

Example 6 :

The scatter plot below shows the profit, by month, for a new company for the first year of operation. Kate drew a line of best fit, as shown in the diagram.

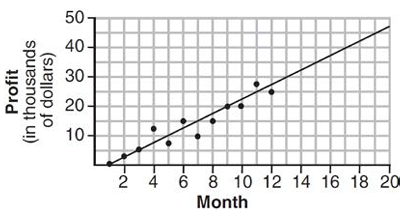
Using this line, what is the best estimate for profit in the 18th month?

1) $35,000     2) $37,750    3) $42,500    4) $45,000

Solution :

x-axis is months and y-axis is profit.

The corresponding value of y is more than 40 thousand but it must be lesser than 45000. Based on this understanding, we choose option 3) $42, 500.

Example 7 :

Based on the line of best fit drawn below, which value could be expected for the data in June 2015?

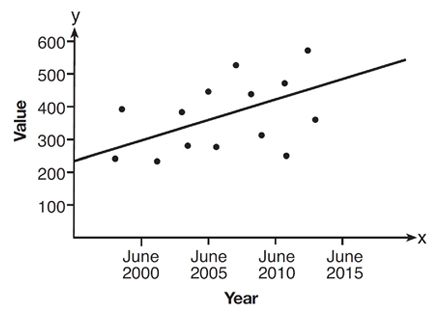
1) 230     2) 310     3) 480      4) 540

Solution :

x-axis represents year and y-axis represents value. The corresponding value of y is lesser than 500. So, option 3) 480 is correct.

The final question on a math test reads, “How many hours did you spend studying for this test?” The teacher records the number of hours each student studied and the grade the student received on the test.

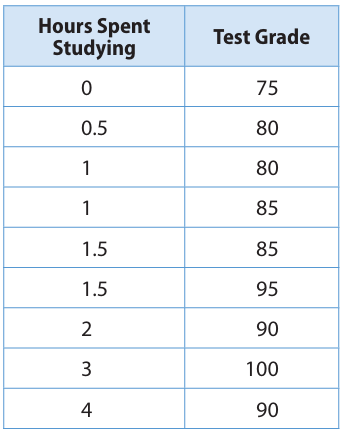
a) Make a prediction about the relationship between the number of hours spent studying and test grades.

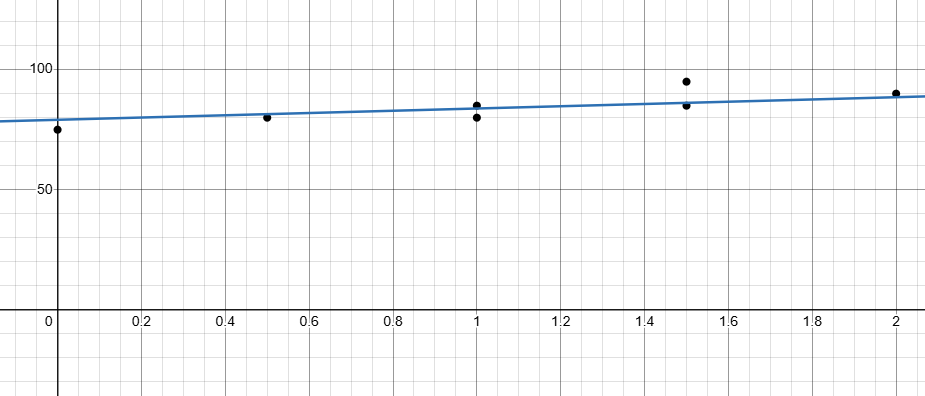
b) Make a scatter plot. Graph hours spent studying as the independent variable and test grades as the dependent variable.

Solution :

a) 

• x - axis - hours spent 
• y - axis = test score

b)  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.