SAT MATH - SOLVING SYSTEMS OF LINEAR EQUATIONS

A set of linear equations with the same two variables is called a system of linear equations. A system of two linear equations can have no solution, one solution, or an infinite number of solutions.

Solving Linear Systems by Graphing

Three types of graphs of linear systems are illustrated below.

1. Intersecting Lines Exactly One Solution :

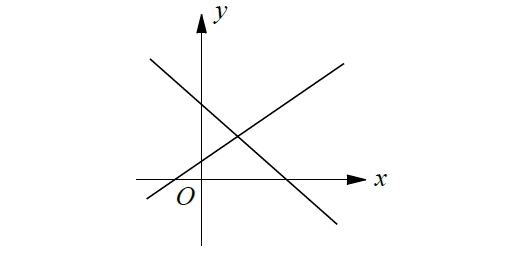
(consistent and independent)

2. Coinciding Lines Infinitely Many Solutions :

(consistent and dependent)

2. Parallel Lines No Solution :

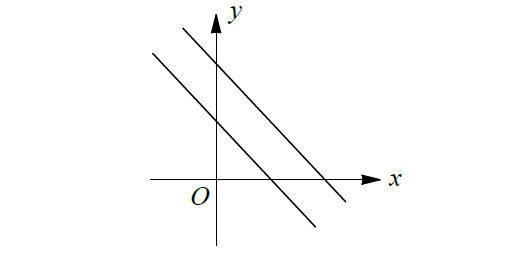
(inconsistent)

Example 1-2 : Solve the system of equations by graphing

Example 1 :

y = 2x

x + 2y = 5

Solution :

y = 2x :

y = 2x has the y-intercept 0 and the slope 2.

Graph (0, 0). From (0, 0), move right 1 unit and up 2 units. Draw a dot. Draw a line through the points.

x + 2y = 5 :

To find x-intercept of x + 2y = 5, substitute y = 0.

x + 2(0) = 5

x + 0 = 5

x = 5

x-intercept is (5, 0)

To find y-intercept of x + 2y = 5, substitute x = 0.

0 + 2y = 5

2y = 5

y = 2.5

y-intercept is (0, 2.5)

Plot (5, 0) and (0, 2.5) 9in a xy-plane and draw a line through these two points.

Example 2 :

-6x + 4y = 8

3x - 2y = -4

Solution :

-6x + 4y = 8 :

Write the equation -6x + 4y = 8 in slope-intercept form.

-6x + 4y = 8

4y = 6x + 8

y = (³⁄₂)x + 2

3x - 2y = -4 :

Write the equation 3x - 2y = -4 in slope-intercept form.

3x - 2y = -4

-2y = -3x - 4

2y = 3x + 4

y = (³⁄₂)x + 2

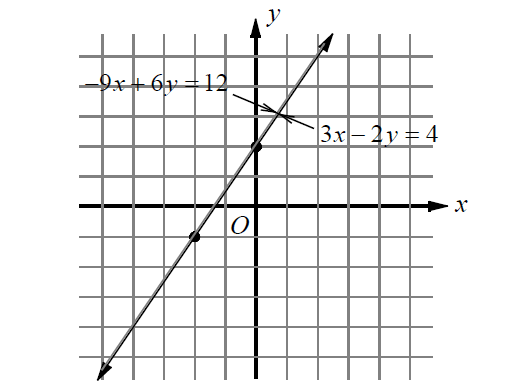
Since the equations are equivalent, their graphs show the same line. Any ordered pair representing a point on that line will satisfy both equations. So, there are infinitely many solutions to this system.

Example 3 :

Solve the following linear system by substitution method.

y = x - 1

2x + y = 5

Solution :

y = x - 1 ----(1)

2x + y = 5 ----(2)

Substitute y = x - 1 in (2).

2x + (x - 1) = 5

2x + x - 1 = 5

3x - 1 = 5

3x = 6

 x = 2

Substitute x = 2 into (1).

y = 2 - 1

y = 1

The solution is (2, 1).

Example 4 :

Solve the following linear system by elimination method.

2x - 3y = 13

-3x + 2y = -12

Solution :

Multiply both sides of the first equation by 3.

3(2x - 3y) = 3(13)

3(2x) - 3(3y) = 3(13)

6x - 9y = 39 ----(1)

Multiply both sides of the first equation by 2.

2(-3x + 2y) = 2(-12)

-6x + 4y = -24 ----(2)

(1) + (2) :

-5y = 15

y = -3

Substitute y = 3 into the first equation.

2x - 3(-3) = 13

2x + 9 = 13

2x = 4

x = 2

The solution is (2, -3).

Example 4 :

For what value of b will the system of linear equations below have no solution?

cx - 2y = 6

3x + 4y = 4

Solution :

Change the equations into slope-intercept form.

y = (ᶜ⁄₂)x - 3

y = (-¾)x + 1

If two equations have the same slope and different y-intercepts, the system has no solution.

The above two equations have different y-intercepts.

If the system has no solution, then the slopes must be equal.

ᶜ⁄₂ = -¾

Multiply both sides by 2.

c = -³⁄₂

Example 4 :

For what value of c will the system of linear equations below have no solution?

-2x + y = 4

5x - by = -10

Solution :

Change the equations into slope-intercept form.

y = 2x + 4

y = (⁵⁄b)x + ¹⁰⁄b

If two equations have infinitely many solutions, they are equivalent. Then, the two equations must have the same slope and same y-intercepts.

Solving the above two equations, we get

b = ⁵⁄₂

Example 5 :

Solve the following linear system.

2x - 3y = 5

y = (⅔)x + 2

Solution :

Write the first equation in slope-intercept form :

2x - 3y = 5

-3y = -2x + 5

y = (⅔)x + ⁵⁄₃

The given linear system :

y = (⅔)x + 2

y = (⅔)x + ⁵⁄₃

The above equations have the same slope, but different y-intercepts.

Therefore, the given linear system has no solution.

Solved Problems

Problem 1 :

y = 2x + 4

x - y = -1

Which ordered pair (x, y) satisfies the system of equations shown above?

(A)  (-2, -3)

(B)  (-1, 2)

(C)  (-3, -2)

(D)  (-2, 0)

Solution :

y = 2x + 4 ----(1)

x - y = -1 ----(2)

Substitute y = 2x + 4 into (2).

x - (2x + 4) = -1

x - 2x - 4 = -1

-x - 4 = -1

Add 4 to both sides.

-x = 3

Multiply both sides by -1.

x = -3

Substitute x = -3 into (1).

y = 2(-3) + 4

y = -6 + 4

y = -2

The solution is (-3, -2).

Therefore, the correct answer is option (C).

Problem 2 :

0.5x + y = 1

-2x - y = 5

If (x, y) is a solution to the system of equations above, what is the value of xy+?

(A) -2

(B)  -1

(C)  1

(D)  2

Solution :

0.5x + y = 1 ----(1)

-2x - y = 5 ----(2)

Adding (1) and (2), y can be eliminated.

-1.5x = 6

Divide both sides by -1.5.

x = -4

Substitute x = -4 into (1).

0.5(-4) + y = 1

-2 + y = 1

Add 2 to both sides.

y = 3.

x + y = -4 + 3

x + y = -1

Therefore, the correct answer is option (B).

Problem 3 :

2x - ky = 14

5x - 2y = 5

In the system of equations above, k is a constant and x and y are variables. For what values of k will the system of equations have no solution?

Solution :

Write the given linear equations in slope-intercept form.

y = (²⁄k)x - ¹⁴⁄k

y = (⁵⁄₂)x - ⁵⁄₂

The system of equations will have no solution, if the two equations have the same slope, different y-intercepts.

²⁄k = ⁵⁄₂

Take reciprocal on both sides.

ᵏ⁄₂ = ⅖

Multiply both sides by 2.

k = ⅘

If k = ⅘, y-intercept of the first equation is

-¹⁴⁄k = -³⁵⁄₂

y-intercept of the second equation is -⁵⁄₂.

When k = ⅘, the two equations have the same slope, but different y-intercepts.

Therefore, the given system will have no solution, when

k = ⅘

Problem 4 :

Which of the following systems of equations has infinitely many solutions?

(A)  x + y = 1  and  x - y = 1

(B)  -2x + y = 1  and  -2x + y = 5

(C)  (½)x - (⅓)y = 1  and  3x - 2y = 6

(B)  2x + 3y = 1  and  3x - 2y = 1

Solution :

Write the equations in each system in slope intercept form and identity the system which contains two equations with same slope and same y-intercept.

Option (A) :

y = -x + 1

y = x - 1

(different slopes and different y-intercepts)

Option (B) :

y = 2x + 1

y = 2x + 5

(same slope, but different y-intercepts)

Option (C) :

y = (³⁄₂)x - 3

y = (³⁄₂)x - 3

(same slope and same y-intercept)

Option (D) :

y = (-⅔)x + ⅓

y = (³⁄₂)x - ½

(different slopes and different y-intercepts)

In option (D), the two equations have the same slope and same y-intercept. So, the system has infinitely many solutions.

Therefore, option (C) is correct.

Problem 5 :

ax - y = 0

x - by = 1

In the system of equations above, a and b are constants and x and y are variables. If the system of equations above has no solution, what is the value of a ⋅ b?

Solution :

Write the equations in the given system in slope intercept form.

y = ax + 0

y = (¹⁄b)x - 1

The above two equations have different y-intercepts.

If the slopes are equal, then the system has no solution.

a = ¹⁄b

Multiply both sides by b.

a ⋅ b = 1

Problem 6 :

2x - (½)y = 15

ax - (⅓)y = 10

In the system of equations above, a is a constant and x and y are variables. For what values of a will the system of equations have infinitely many solution?

Solution :

Write the equations in the given system in slope intercept form.

y = 4x - 30

y = 3ax - 30

The above two equations have same y-intercept.

If the slopes are equal, then the system has infinitely many solutions.

3a = 4

Divide both sides by 3.

a = ⁴⁄₃

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.