SAT MATH - SOLVING INEQUALITIES

An inequality is a mathematical sentence that contains inequality symbols such as

>, <, ≥, ≤

between numerical or variable expressions. Four types of simple inequalities and their graphs are shown below.

Verbal Expression :

All real numbers less than 4.

Inequality :

x < 4

Graph :

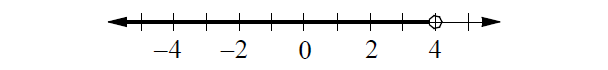
Verbal Expression :

All real numbers greater than -3.

Inequality :

x > -3

Graph :

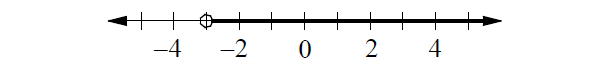
Verbal Expressions :

All real numbers less than or equal to 2.

All real numbers at most 2.

All real numbers no greater than 2.

Inequality :

x ≤ 2

Graph :

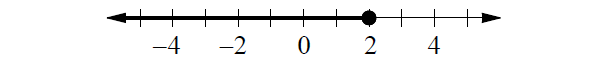
Verbal Expressions :

All real numbers greater than or equal to -1.

All real numbers at least -1.

All real numbers no less than -1.

Inequality :

x ≥ -1

Graph :

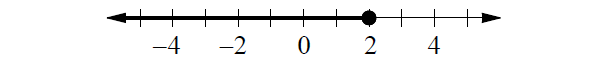
Notice on the graphs that we use an open dot for > or < and a solid dot for ≥ or ≤.

Properties of Inequalities

For all real numbers a, b, and c, the following are true.

Transitive Property :

If a < b and b < c, then a < c.

Addition Property :

If a < b, then a + c < b + c.

Subtraction Property :

If a < b, then a - c < b - c.

Multiplication Property :

If a < b and c is positive, then a ⋅ c < b ⋅ c.

Division Property :

If a < b and c is positive, then ᵃ⁄c < ^b⁄c.

Note :

Whne you multiply or divide both sides of an inequality by the same negaive number, you have to flip the inequality sign.

Examples :

2 < 3 ----> 2 ⋅ (-1) > 3 ⋅ (-1) ----> -2 > -3

2 < 3 ----> ²⁄₍₋₁₎ > ³⁄₍₋₁₎ ----> -2 > -3

Solved Problems

Problem 1 :

(a) The number x is no greater than -2.

(b) The amount of calories n meet or exceed 1,200.

Solution :

Part (a) :

x ≤ -2

Part (a) :

n ≥ 1200

Problem 2 :

Solve for n.

4n - 9 ≥ 12 - 3n

Solution :

4n - 9 ≥ 12 - 3n

Add 3n to both sides.

7n - 9 ≥ 12

Add 9 to both sides.

7n ≥ 21

Divide both sides by 7.

n ≥ 3

Problem 3 :

If -3 + n ≤ 25, which inequality represents the possible range of values for 4n - 12?

(A)  4n - 12 ≤ -100

(B)  4n - 12 ≤ 100

(C)  4n - 12 ≥ -100

(D)  4n - 12 ≥ -100

Solution :

-3 + n ≤ 25

Add 3 to both sides.

n ≤ 28

Multiply both sides by 4.

4n ≤ 112

Subtract 12 from both sides.

4n - 12 ≤ 100

Therefore, the correct answer is option (B).

Problem 4 :

Which of the following numbers is NOT a solution to the inequality (½)x - ⅓ > ⁷⁄₉ + (⁵⁄₂)x? 

(A)  -⁷⁄₂

(B)  -⁵⁄₂

(C)  -³⁄₂

(D)  -½

Solution :

(½)x - ⅓ > ⁷⁄₉ + (⁵⁄₂)x

Multiply both sides by 2.

2[(½)x - ⅓] > 2[⁷⁄₉ + (⁵⁄₂)x]

2[(½)x] - 2[⅓] > 2[⁷⁄₉] + 2[(⁵⁄₂)x]

x - ⅔ > ¹⁴⁄₉ + 5x

Multiply both sides by 9.

9[x - ⅔] > 9[¹⁴⁄₉ + 5x]

9x - 9(⅔) > 9(¹⁴⁄₉) + 9(5x)

9x - 6 > 14 + 45x

Subtract 9x from both sides.

-6 > 14 + 36x

Subtract 14 from both sides.

-20 > 36x

Divide both sides by 36.

-⁵⁄₉ > x

x < -⁵⁄₉

x < -0.56

In option (D), -½ = -0.5 which is greater than -0.56.

-½ is not a solution to the inequality. 

Therefore, the correct answer is option (D).

Problem 5 :

-3a + 7 ≥ 5a - 17

In the inequality shown above, find the greatest possible value of 3a + 7.

(A)  16

(B)  14

(C)  12

(D)  10

Solution :

-3a + 7 ≥ 5a - 17

Add 3a to both sides.

7 ≥ 8a - 17

Add 17 to both sides.

24 ≥ 8a

Divide both sides by 8.

3 ≥ a

a ≤ 3

Multiply both sides by 3.

3a ≤ 9

Add 7 to both sides.

3a + 7 ≤ 16

3a + 7 can be equal to 16 or less than 16.

The greatest possible value of 3a + 7 is 16.

Therefore, the correct answer is option (A).

Problem 6 :

Nine is not more than the sum of a number and 17.

Which of the following inequalities represents the statement above?

(A)  9 ≥ 17x

(B)  9 ≥ x + 17

(C)  9 ≤ 17x

(D)  9 ≤ x + 17

Solution :

Let x be the number.

The inequality represents the given statement :

9 ≤ x + 17

Therefore, the correct answer is option (D).

Problem 7 :

The product of 7 and number y is no less than 91.

Which of the following inequalities represents the statement above?

(A)  7y ≤ 91

(B)  7y < 91

(C)  7y ≥ 91

(D)  7y > 91

Solution :

Let x be the number.

The inequality represents the given statement :

7y ≥ 91

Therefore, the correct answer is option (C).

Problem 8 :

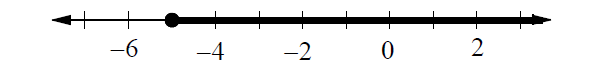
Which of the following inequalities represents the graph above?

(A)  m ≤ -5

(B)  m < -5

(C)  m ≥ -5

(D)  m > -5

Solution :

In the above graph, it is clear that the value of the variable m is equal to -5 or greater than -5.

m ≥ -5

Therefore, the correct answer is option (C).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.