SAT MATH - RATE OF CHANGE AND SLOPE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The average rate of change is a ratio that describes, on average, change in one quantity with respect to change in another quantity. If x is the independent variable and y is the dependent variable, then the average rate of change
Geometrically, the rate of change is the slope of the line through the points (x1, y1) and (x2, y2).
The slope m of a line through (x1, y1) and (x2, y2) is
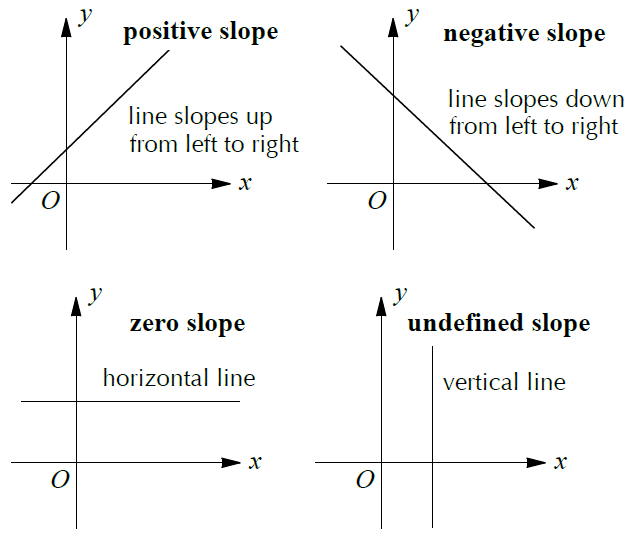
Slope intercept form equation of a line :
y = mx + b
m ----> slope
b ----> y-intercept
Equation of a line in general form :
ax + by + c = 0
Equation of a line in standard form :
ax + by = c
Let the equation of a line be given in general form or standard form. If you want to find the slope of the line, write the equation of the line in slope intercept form and find the slope.
Solved Problems
Problem 1 :
Find the slope of the line that passes through (3, -2) and (-5, 4).
(A) ¾
(B) -¾
(C) ½
(D) -½
Solution :
Formula to find the slope of a line joining two points :
Substitute (x1, y1) = (3, -2) and (x2, y2) = (-5, 4).
Therefore, the correct answer is option (B).
Problem 2 :
Find the slope of the line that passes through (-1, -8) and (3, 2).
(A) ⁵⁄₂
(B) -⁵⁄₂
(C) ⁵⁄₃
(D) -⁵⁄₃
Solution :
Formula :
Substitute (x1, y1) = (-1, -8) and (x2, y2) = (3, 2).
Therefore, the correct answer is option (A).
Problem 3 :
Find the slope of the line shown below.
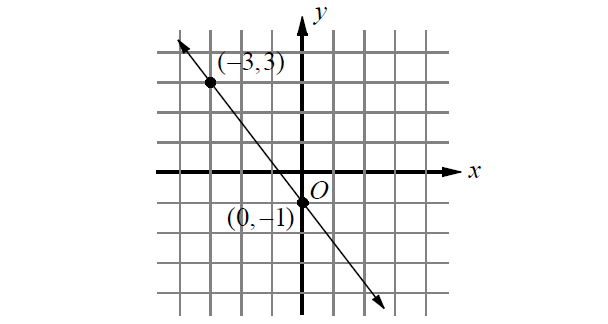
(A) ⁴⁄₃
(B) -¾
(C) ¾
(D) -⁴⁄₃
Solution :
Formula :
Substitute (x1, y1) = (-3, 3) and (x2, y2) = (0, -1).
Therefore, the correct answer is option (D).
Problem 4 :
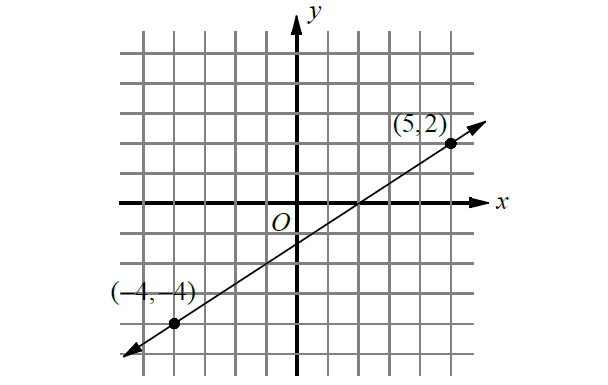
What is the rate of change shown in the graph of the line above?
(A) ⅔
(B) -³⁄₂
(C) ³⁄₂
(D) -⅔
Solution :
Average rate of change :
Therefore, the correct answer is option (A).
Problem 5 :
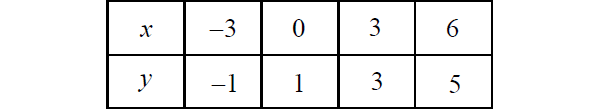
What is the average rate of change for the relation shown in the table above?
(A) -⅔
(B) ⅔
(C) -³⁄₂
(D) ⅔
Solution :
Take any two points from the table.
Let's take (-3, -1) and (6, 5).
Average rate of change :
Therefore, the correct answer is option (B).
Problem 6 :
A line passes through the points (4, 3) and (-5, k). If the line has a slope of -1, find the value of k.
Solution :
slope = -1
Substitute (x1, y1) = (4, 3) and (x2, y2) = (-5, k).
k - 3 = 9
k = 12
Problem 7 :
If the line that passes through (a, 7) and (1, a) has a slope of -⁵⁄₉, what is the value of a?
Solution :
Substitute (x1, y1) = (a, 7) and (x2, y2) = (1, a).
By cross-multiplication,
9(a - 7) = -5(1 - a)
9a - 63 = -5 + 5a
4a - 63 = -5
4a = 58
a = ⁵⁸⁄₄
a = ²⁹⁄₂
Problem 8 :
The graph of the linear function f passes through the points (a, 1) and (1, b) in the xy-plane. If the slope of the graph of f is 1, which of the following is true?
(A) a - b = 1
(B) a + b = 1
(C) a - b = 2
(D) a + b = 2
Solution :
slope = 1
Substitute (x1, y1) = (a, 1) and (x2, y2) = (1, b).
b - 1 = 1 - a
a + b - 1 = 1
a + b = 2
Therefore, the corect answer is option (D).
Problem 9 :
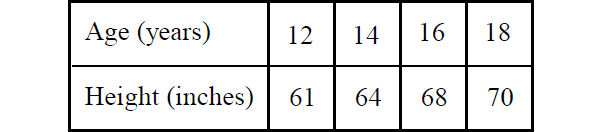
The table above shows Abraham’s height from age 12 to 18. Find the average rate of change in Abraham’s height from age 12 to 18.
Solution :
Average rate of change in Abraham's height from age 12 to 18 :
= 1.5 inches per year
Problems 10-13 : Find the slope of the line in the equation.
Problem 10 :
3x + y - 5 = 0
Solution :
The given equation is in general form. To find the slope, write the given equation in slope-intercept form.
3x + y - 5 = 0
Subtract 3x from both sides.
y - 5 = -3x
Add 5 to both sides.
y = -3x + 5
If the above equation is compared to y = mx + b,
m = -3
slope = -3
Problem 11 :
2x + 3y = 6
Solution :
The given equation is in standard form. To find the slope, write the given equation in slope-intercept form.
2x + 3y = 6
Subtract 2x from both sides.
3y = -2x + 6
Divide both sides by 3.
y = ⁽⁻²ˣ ⁺ ⁶⁾⁄₃
y = (⁻²ˣ⁄₃) + ⁶⁄₃
y = (⁻²⁄₃)x + 2
If the above equation is compared to y = mx + b,
m = -²⁄₃
slope = -²⁄₃
Problem 12 :
5x - y = -2
Solution :
The given equation is in standard form. To find the slope, write the given equation in slope-intercept form.
5x - y = -2
Subtract 5x from both sides.
-y = -5x - 2
Multiply both sides by -1.
-1(-y) = -1(-5x - 2)
y = 5x + 2
If the above equation is compared to y = mx + b,
m = 5
slope = 5
Problem 13 :
-x + 4y - 6 = 0
Solution :
The given equation is in general form. To find the slope, write the given equation in slope-intercept form.
-x + 4y - 6 = 0
Add x to both sides.
4y - 6 = x
Add 6 to both sides.
4y = x + 6
Divide both sides by 4.
y = ⁽ˣ ⁺ ⁶⁾⁄₄
y = ˣ⁄₄ + ⁶⁄₄
y = (¼)x + ³⁄₂
If the above equation is compared to y = mx + b,
m = ¼
slope = ¼
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
