SAT MATH QUESTIONS WITH ANSWERS
(Part - 1)

Question 1 :

If a/b = 2, what is the value of 4b/a?

(A) 0

(B) 1

(C) 2

(D) 4

Answer :

a/b = 2

Take reciprocal on both sides.

b/a = 1/2

Multiply both sides by 4.

4(b/a) = 4(1/2)

4b/a = 4/2

4b/a = 2

The correct answer choice is (C).

Question 2 :

If x > 3, which of the following is equivalent to

Answer :

The correct answer choice is (B).

Question 3 :

The price of a textbook this year is 20% greater than the price last year. If this year's price is p, what was last year's price in terms of p?

(A) p/5

(B) 4p/5

(C) 5p/6

(D) 6p/5

Solution :

Let be last year's price of the text book.

Given : The price of a textbook this year is 20% greater than the price last year and this year's price is p.

p = (100 + 20)% of x

or

(100 + 20)% of x = p

120% of x = p

1.2x = p

Divide both sides by 1.2.

x = p/1.2

x = 10p/12

x = 5p/6

The correct answer choice is (C) 5p/6.

Question 4 :

If k > 0 and x = 7 in the equation above, what is the value of k?

(A) 2

(B) 3

(C) 4

(D) 5

Answer :

Add x to both sides.

Square both sides.

2k² + 17 = x²

Substitute x = 7.

2k² + 17 = 7²

2k² + 17 = 49

Subtract 17 from both sides.

2k² = 32

Divide both sides by 2.

k² = 16

Take square root on both sides.

√k² = √16

k = ±4

k = 4  or  k = 4

Since k > 0, k = 4.

The correct answer choice is (C).

Question 5 :

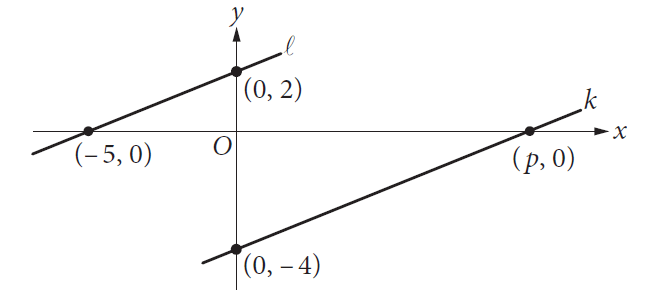
In the xy-plane above, line ℓ is parallel to line k. What is the value of p?

(A) 4

(B) 5

(C) 8

(D) 10

Answer :

Formula for slope of a line joining (x₁, y₁) and (x₂, y₂) :

Slope of line ℓ :

Substitute (x₁, y₁) = (-5, 0) and (x₂, y₂) = (0, 2) into the above formula.

Slope of line k :

Substitute (x₁, y₁) = (0, -4) and (x₂, y₂) = (p, 0) into the above formula.

Since line ℓ is parallel to line k, the slopes must be equal.

The correct answer choice is (D).

Question 6 :

The graph of a line in the xy-plane has slope 2 and contains the point (1, 8). The graph of a second line passes through the points (1, 2) and (2, 1). If the two lines intersect at the point (a, b), what is the value of a + b?

(A) 4

(B) 3

(C) -1

(D) -4

Solution :

Equation of the line which has slope 2 and contains the point (1, 8) :

y = mx + b

Substitute m = 2.

y = 2x + b

Since the line contains the point (1, 8), substitute x = 1 and y = 8 to solve for b.

8 = 2(1) + b

8 = 2 + b

Subtract 2 from both sides.

6 = b

Equation of the first line :

y = 2x + 6 ----(1)

Equation of the line passes through the points (1, 2) and (2, 1) :

Formula for slope of a line joining (x₁, y₁) and (x₂, y₂) :

Substitute (x₁, y₁) = (1, 2) and (x₂, y₂) = (2, 1) into the above formula.

Equation of a line in slope-intercept form :

y = mx + b

Substitute m = -1.

y = -x + b

Since the line passes through the point (1, 2), substitute x = 1 and y = 2.

2 = -1 + b

Add 1 to both sides.

3 = b

Equation of the second line :

y = -x + 3 ----(2)

Solve (1) and (2).

y = y

2x + 6 = -x + 3

Add x to both sides.

3x + 6 = 3

Subtract 6 from both sides.

3x = -3

Divide both sides by 3.

x = -1

Substitute x = -1 in (2).

y = -(-1) + 3

y = 1 + 3

y = 4

The point of intersection is (-1, 4).

Given : The two lines intersect at the point (a, b).

(a, b) = (-1, 4)

a = -1  and  b = 4

a + b = -1 + 4

a + b = 3

The correct answer choice is (B).

Question 7 :

A website uses the formula above to calculate a seller’s rating, R, based on the number of favorable reviews, F, and unfavorable reviews, N. Which of the following expresses the number of favorable reviews in terms of the other variables?

Solution :

The correct answer choice is (A).

Question 8 :

A radioactive substance decays at an annual rate of 13 percent. If the initial amount of the substance is 325 grams, which of the following functions f models the remaining amount of the substance, in grams, t years later?

(A)  f(t) = 325(0.87)^t

(B)  f(t) = 325(0.13)^t

(C)  f(t) = 0.87(325)^t

(D)  f(t) = 0.13(325)^t

Answer :

Formula for exponential decay :

f(t) = a(1 - r)^t

a ----> Initial amount of the substance

r ----> Annual decay rate

t ----> time in years

f(t) ----> Amount of substance after t years

So, a = 325, r = 13% or 0.13.

f(t) = 325(1 - 0.13)^t

f(t) = 325(0.87)^t

The correct answer choice is (A).

Question 9 :

The sales manager of a company awarded a total of $3000 in bonuses to the most productive salespeople. The bonuses were awarded in amounts of $250 or $750. If at least one $250 bonus and at least one $750 bonus were awarded, what is one possible number of $250 bonuses awarded?

Answer :

Let x be the number of $250 and y be the number of $750.

Since x and y represent number of bonuses, they can be only positive integers.

Since there were at least one $250 bonus and at least one $750 bonus  awarded,

x ≥ 1  and  y ≥ 1

Given : Total bonus awarded is $3000.

250x + 750y = 3000

250(x + 3y) = 3000

Divide both sides by 250.

x + 3y = 12

If x = 1,

1 + 3y = 12

3y = 11

y = 3.666.... (not an integer)

If x = 2,

2 + 3y = 12

3y = 10

y = 3.333.... (not an integer)

If x = 3,

3 + 3y = 12

3y = 9

y = 3.... (an integer)

So, x = 3 can be accepted.

One possible number of $250 bonuses awarded is 3.

Question 10 :

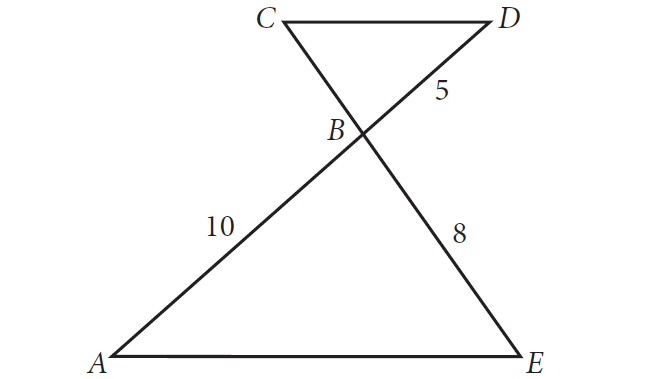
In the figure above, AE || CD and segment AD intersects segment CE at B. What is the length of segment CE?

Answer :

Let x be the length of CB.

Then,

CE = CB + BE

CE = x + 8

Given : AE || CD.

Segments AD and EC are transversals.

∠A and ∠D are alternate interior angles, 

m∠A = m∠D

∠E and ∠C are alternate interior angles, 

m∠E = m∠C

m∠A and m∠E of ΔAEB are equal to m∠D and m∠C ΔDCB respectively.

By AA Similarity Postulate, ΔAEB and ΔDCB are similar triangles.

Then, the corresponding sides are proportional.

CE = x + 8

Substitute x = 4.

CE = 4 + 8

CE = 12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.