SAT MATH QUESTIONS WITH ANSWERS
(Part - 5)

Question 1 :

If a + b = c, which of the following is equal to a² + b²?

(A)  c + 2ab

(B)  c²

(C)  c² - ab

(D)  c² - 2ab

Answer :

a + b = c

Squaring both sides,

(a + b)² = c²

(a + b)(a + b) = c²

a² + ab + ab + b² = c²

a² + 2ab + b² = c²

a² + b² = c² - 2ab

Therefore, the correct answer is option (D).

Question 2 :

If ᵐ⁄n = ⅔, what is the value of ²ⁿ⁄m + 5?

Solution :

ᵐ⁄n = ⅔

ⁿ⁄m = ³⁄₂

 ²ⁿ⁄m + 5 = 2(ⁿ⁄m) + 5

Substitute ⁿ⁄m = ³⁄₂.

 = 2(³⁄₂) + 5

 = 3 + 5

 = 8

Question 3 :

If k is an integer constant greater than 1, which of the following values of x satisfies the inequality ˣ⁄₃ + 1 ≥ k?

(A)  k - 3

(B)  k

(C)  3k - 4

(D)  3k - 2

Solution :

ˣ⁄₃ + 1 ≥ k

Since k is an integer constant greater than 1, let k = 2.

ˣ⁄₃ + 1 ≥ 2

ˣ⁄₃ ≥ 1

x ≥ 3

When k = 2, x ≥ 3.

In each of the given options, substitute k = 2 and check where you get the value ≥ 3.

(A) ---> k - 3 = 2 - 3 = -1 

(B) ----> k = 2

(C) ----> 3k - 4 = 3(2) - 4 = 2

(D) ----> 3k - 2 = 3(2) - 2 = 4 ≥ 3

Therefore, the correct answer is option (D).

Question 4 :

If r + 9 is 4 more than s, then r - 11 is how much less than s?

(A)  9

(B)  11

(C)  16

(D)  20

Solution :

Given : r + 9 is 4 more than s.

r + 9 = s + 4

r = s - 5

r - 11 = s - 16

r - 11 is 16 less than s.

Therefore, the correct answer is option (C).

Question 5 :

If x < y and -3x > y, which of the following must be true?

(A)  x < 0

(B)  y > 0

(C)  |x| > y

(D)  x² > y

Solution :

Assume some value for x and y such that x < y and -3x > y.

both x and y are positive

x is negative and y is positive

both x and y are negative

The possible values we can have for x and y :

x = 1  and  y = 2

x = -1  and  y = 1

x = -2  and  y = -1

Case (i) :

When x = 1 and y = 2, options (A) and (B) are true.

Case (ii) :

When x = -1 and y = 1, options (A) and (B) are true.

Case (ii) :

When x = -2 and y = -1, options (A), (C) and (D) are true.

In all the three cases, option (A) only is true.

Therefore, the correct answer is option (A).

Question 6 :

If Brunhilda went to casino and lost 40% of her money playing Pai Gow poker before doubling her remaning money playing roulette, the amount of money she had after playing roulette is what percent is what percent of the amount of money she started with? 

(A)  20%

(B)  80%

(C)  100%

(D)  120%

Solution :

Let x $100 be the money Brunhilda started with.

After having lost 40% of the money by playing Pai Gow poker,

= (100 - 40)% ⋅ $100

= 60% ⋅ $100

= 0.6 ⋅ $100

= $60

After having doubled the money by playing roulette,

= 2($60)

= $120

$120 is 120% of $100, the money Brunhilda started with.

Therefore, the correct answer is option (D).

Question 7 :

If 2x + y = 8 and x < 7, which of the following must be true?

(A)  y > -6

(B)  y < -6

(C)  -6 < y < 7

(D)  y < 6

Solution :

2x + y = 8

Solve for x.

2x = 8 - y

x = ⁽⁸ ⁻ ʸ⁾⁄₂

⁽⁸ ⁻ ʸ⁾⁄₂ = x

⁽⁸ ⁻ ʸ⁾⁄₂ = x < 7

⁽⁸ ⁻ ʸ⁾⁄₂ < 7

8 - y < 14

-y < 6

y > -6

Therefore, the correct answer is option (A).

Question 8 :

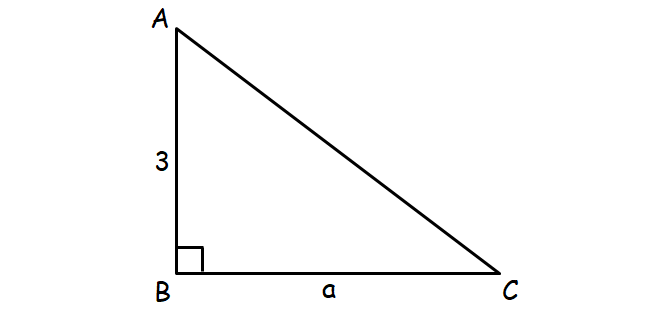
The figure above shows the right triangle ABC with legs of length 3 and a. What is the value of sinA?

Solution :

In the given right triangle, find the length of hypotenuse using Pythagorean Theorem.

AC² = AB² + BC²

AC² = 3² + a²

AC² = 9 + a²

Taking square root on both sides,

Find the value of sinA.

Therefore, the correct answer is option (C).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.