SAT MATH QUESTIONS WITH ANSWERS
(Part - 4)

Question 1 :

In three plays, a football team loses 5 yards and then gains 32 yards by completing a pass. Then  a penalty was called and the team lost 10 yards. How many yards did the team actually gain?

Answer :

= -5 + 32 - 10

= 17 yards

Question 2 :

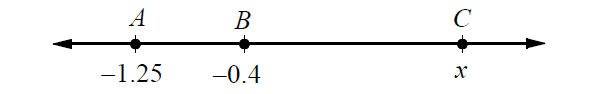
On the number line above, if BC = 2AB, find the value x.

Answer :

Length of BC :

BC = C - B

BC = x - (-0.4)

BC = x + 0.4

Length of AB :

AB = B - A

AB = -0.4 - (-1.25)

AB = -0.4 + 1.25

AB = 0.85

Given : BC = 2AB.

x + 0.4 = 2(0.85)

x + 0.4 = 1.7

Subtract 0.4 from both sides.

x = 1.3

Question 3 :

If n > 0, how much is (n + 3) greater than (n - 11)?

(A)  8
(B)  10
(C)  12
(D)  14

Answer :

To know know how much (n + 3) is greater than (n - 11), subtract the smaller value from the greater value.

= (n + 3) - (n - 11)

= n + 3 - n + 11

= 14

Therefore, (n + 3) is greater than (n - 11) by 14.

The correct answer is option (D).

Question 4 :

What number is halfway between -⅚ between ⅓?

(A)  -¼
(B)  -⅓
(C)  -½
(D)  -⁵⁄₁₂

Answer :

To find a number which is halfway between -⅚ between ⅓ is to find the average of the given two numbers.

Average of -⅚ and ⅓ :

The correct answer is option (A).

Question 5 :

How many minutes are there in 2h hours and 6m minutes?

(A)  60h + 12m

(B)  120h + 6m

(C)  60h + 6m

(D)  120h + 60m

Answer :

To find the number of minutes in 2h hours and 6m minutes, convert 2h hours to minutes.

Since 1 hour = 60 minutes, we have to multiply 2h hours by 60 to convert it to minutes.

2h hours and 6m minutes :

= 2h hours + 6m minutes

= 2h ⋅ 60 minutes + 6m minutes

= 120h minutes + 6m minutes

= (120h + 6m) minutes

The correct answer is option (B).

Question 6 :

If x = 10, what is the value of ˣ⁄₂ + ˣ⁄₂₀ + ˣ⁄₂₀₀? 

Answer :

= ˣ⁄₂ + ˣ⁄₂₀ + ˣ⁄₂₀₀

Substitute x = 10.

= ¹⁰⁄₂ + ¹⁰⁄₂₀ + ¹⁰⁄₂₀₀

= 5 + ⁵⁰⁄₁₀₀ + ⁵⁰⁄₁₀₀₀

= 5 + 0.5 + 0.05

= 5.55

Question 7 :

If x and y are positive integers and 2x + 5y = 18, what is the value of x?

Answer :

Since both x and y are posoitve integers,

x = 1, 2, 3,.......

y = 1, 2, 3,.......

We can test the values 1, 2, 3,....... one by one for x.

When x = 1,

2(1) + 5y = 18

2 + 5y = 18

5y = 16

y = ¹⁶⁄₅ (not an integer)

When x = 2,

2(2) + 5y = 18

4 + 5y = 18

5y = 14

y = ¹⁴⁄₅ (not an integer)

When x = 3,

2(3) + 5y = 18

6 + 5y = 18

5y = 12

y = ¹²⁄₅ (not an integer)

When x = 4,

2(4) + 5y = 18

8 + 5y = 18

5y = 10

y = 2 (positive integer)

Therefore,

x = 4

Question 8 :

The sum of four consecutive odd integers is 296. What is the greatest of the four consecutive odd integers?

Answer :

For example, if 5 is the first odd integer, then the four consecutive odd integers are

5, 7, 9, 11

But, we do not the first odd integer. So, we can assume x as the first odd integer. Then the four consecutive integers are 

x, x + 2, x + 4, x + 6

Given :  The sum of four consecutive odd integers is 296.

x + (x + 2) + (x + 4) + (x + 6) = 296

x + x + 2 + x + 4 + x + 6 = 296

4x + 12 = 296

Subtract 12 from both sides.

4x = 284

Divide both sides by 4.

x = 71

The greatest of four consecutive odd integers :

= x + 6

Substitute x = 71

= 71 + 6

= 77

Verify :

When x = 71, the four consecutive odd integers,

71, 73, 75, 77

Sum of the four consecutive odd integers :

= 71 + 73 + 75 + 77

= 296 (verified)

Question 9 :

The product of four consecutive positive integers is 120. Find the smallest of the four consecutive positive integers. 

Answer :

Let us assume the following are the four positive consecutive positive integers.

y, y + 1, y + 2, y + 3

Given : The product of four consecutive positive integers is 120.

y(y + 1)(y + 2)(y + 3) = 120

Solving the above equation for y is a difficult process. Because,  if you multiply the terms on the left side, the exponent of y is 4. Try to write 120 as a product of four consecutive positive integers in ascending order (smallest to greatest).

y(y + 1)(y + 2)(y + 3) = 2 ⋅ 60

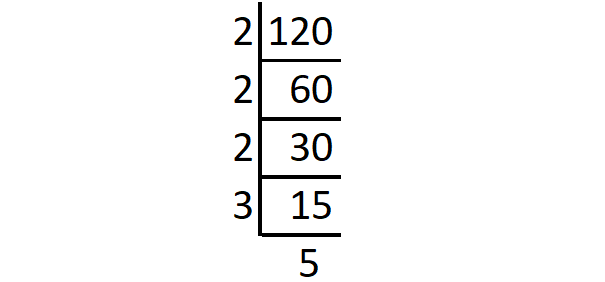
y(y + 1)(y + 2)(y + 3) = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5

y(y + 1)(y + 2)(y + 3) = 2 ⋅ 3 ⋅ (2 ⋅ 2) ⋅ 5

y(y + 1)(y + 2)(y + 3) = 2 ⋅ 3 ⋅ 4 ⋅ 5

Comparing the smallest values on both sides,

y = 2

The smallest of the four consecutive positive integers is 2.

Question 10 :

Find the sum of all three digit numbers which can be formed with the digits 3, 5 and 7, if each digit is used only once in each arrangement. 

Answer :

The list of three digit numbers which can be formed with the digits 3, 5 and 7 (each digit is used only once in each arrangement).

357

375

537

573

735

753

Sum of the above three digit numbers is 3330. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.