SAT MATH QUESTIONS WITH ANSWERS
(Part - 3)

Question 1 :

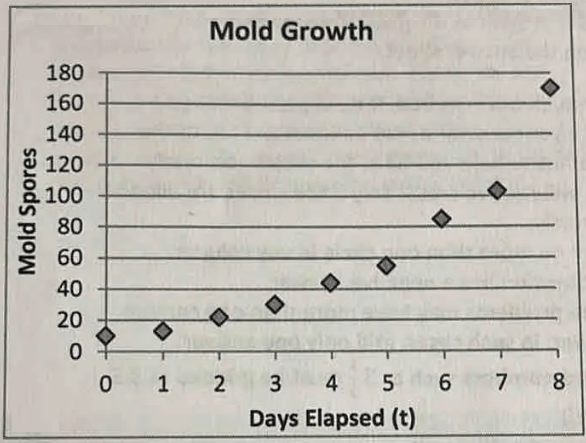
A biologist measures the growth in the number of mold spores in a petri dish every day for 8 days. The results are shown in the figure above.

If t represents the number of days since the start of the experiment and m represents the number of mold spores counted on that day, which of the following functions best models the data shown in the figure above?

Answer :

In the given graph, the vertical-intercept is about 10.

That is, when t = 0, m = 10.

In option (B), when t = 0, m = 0. So, option (B) can be rejected.

In the graph, when t = 1, the value of m is between 10 and 20.

In option (D), when t = 1, m = 20. Moreover, in option (D), when t = 2, m = 40. In the graph, when t = 2, m is slightly above 20. So, option (D) can be rejected.

In option (A), when t = 2, m = 14. So, option (A) can be rejected.

In option (C),

t = 0 ----> m = 10

t = 2 ----> m = 20

t = 4 ----> m = 40

t = 6 ----> m = 80

The above workings on option (C) match with the given graph.

Therefore, option (C) is correct.

Question 2 :

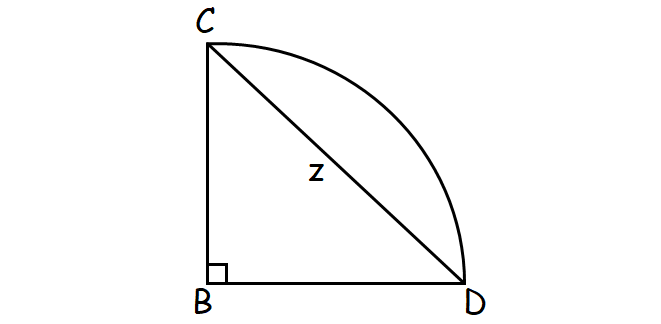
In the figure above, the length of arc CD, which is centered at B, is 12π. What is z?

(A) 12√2

(B) 24

(C) 24√2

(D) 48

Answer :

Length of arc CD = 12π

In the picture shown above, BC and BD are radii.

BC = BD = 24

In the right triangle CBD, by Pythagorean theorem,

CD² = BC² + BD²

z² = 24² + 24²

z² = 576 + 576

z² = 1152

z = √1152

z = 24√2

Therefore, option (C) is correct.

Question 3 :

In 2013, Sam earned $120,000 in income and made $10,000 in purchases. However, he did not own any property. How much tax did he pay, in dollars?

Answer :

Income Tax :

Sam spent $10,000 in purchses. Since he did not own any property, he did not purchase any property in $10,000 purchases.

So, we have nothing to subtract from the income $120,000.

From the instructions given above, Sam's income $120,000 can be splitted into three parts.

$20,000 + $80,000 + $20,000

The first part of income $20,000 is not taxed.

The second part of income $80,000 is taxed at a rate of 6%.

0.06 ⋅ $80,000 = $4800

The third part of income $20,000 is taxed at a rate of 12%.

0.12 ⋅ $20,000 = $2400

Total income tax = $4800 + $2400 = $7200

Sales Tax :

All purchases (including property purchases) are taxed at a rate of 5%.

Sam spent $10,000 for purchases. But he did not purchase any property.

0.05 ⋅ $10,000 = $500

Total tax paid by Sam in 2013 :

= $7200 + $500

= $7700

Question 4 :

In 2014, Sam earned the same amount in income and made the same amount of non-property purchases. However, he also purchased $50,000 worth of property. By paying the sales tax and property tax on this purchase but deducting the purchase from his income tax, how much lower were his total taxes, in dollars, compared to the previous year?

Answer :

Income Tax :

Sam purchased $50,000 worth of property.

Net income = $120,000 - $50,000

= $70,000

Sam's income $70,000 can be splitted into two parts.

$20,000 + $50,000

The first part of income $20,000 is not taxed.

The second part of income $50,000 is taxed at a rate of 6%.

= 0.06 ⋅ $50,000

= $3000

Sales Tax :

Total purchase = $10,000 + $50,000

= $60,000

Sales tax = = 0.05 ⋅ $60,000

= $3000

Property Tax :

All property is taxed at a rate equal to 1% of the most recent purchase price of the property.

0.01 ⋅ $50,000 = $500

Total tax paid by Sam in 2014 :

= $3000 + $3000 + $500

= $6500

This is lower than the previous year tax by

= $7700 - 6500

= $1200

Question 5 :

A wooden rectangular solid has a square base with side length 6 cm and height a of 10 cm. A round hole of diameter 4 cm is cut through the solid from top to bottom. If the density of the wood is 0.7g/cm3, what is the mass of the remaning wooden figure, to the nearest gram? (Density is mass divided by volume ; us 3.14 for π.)

Answer :

Volume of the rectangular solid :

= 6 ⋅ 6 ⋅ 10

= 360 cm³

A round hole of diameter 4 cm (radius 2 cm) is cut through the solid from top to bottom will be in the shape of a cylinder. Height of the cylinder is the height of the rectangular solid, that is 10 cm.2

Volume of the solid from the hole :

= volume of the cylinder

= πrr²h

= 3.14 ⋅ 2² ⋅ 10

= 125.6 cm³

Volume of the rmeaning solid :

= (360 - 125.6) cm³

= 234.4 cm³

Given : Density of the wood is 0.7g/cm³.

Mass of the remaining wooden figure :

= 234.4(0.7) g

≈ 164 g

Use the following information for questions 6 and 7.

A cash for gold website operates by getting customers to mail gold to the sites processing facility. There, the gold is weighed and checked for purity. The weight and purity levels are used to compute the market value of the gold. The website then sends customer a check for the gold's value minus a 15% fee.

The market values for gold of different purity levels (in karats) are given in the table below.

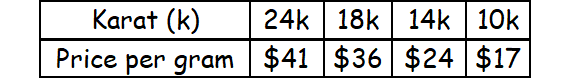
Cynthia sends a necklace made of 18-karat gold to the website. She receives a check for $137.70 in return.

Question 6 :

What was the weight (in grams) of Cynthia's necklace?

Answer :

Let x be the weight of Cynthia's necklace.

Given : Cynthia's neckalce made of 18 karat gold

Value of the neckalce :

= Value per gram ⋅ Weight

= $36 ⋅ x

= 36x

After 15% fee,

= (1 - 0.15) ⋅ 36x

= 0.85 ⋅ 36x

= 30.6x

Given : She receives a check for $137.70 in return.

30.6x = 137.70

x = 4.5

The weight of Cynthia's necklace was 4.5 grams.

Question 7 :

Cynthia also has a collection of gold bracelets ; each weighs 1.1 grams. However, she does not know the purity of the gold in the bracelets. If she sends 7 of the bracelets. If she sends 7 of the bracelets in to the website, what is the difference (rounded to the nearest dollar) between the largest amount she could get in return and the smallest amount?

Answer :

Total weight of the 7 bracelets :

= 7 ⋅ 1.1

= 7.7 grams

When the purity of the gold in the bracelets is 24-karat, Cynthia will the largest amount.

The largest amount :

= 7.7 ⋅ 41

= $315.7

After 15% fee,

= (1 - 0.15) ⋅ 315.7

= 0.85 ⋅ 315.7

= $268.345

When the purity of the gold in the bracelets is 10-karat, Cynthia will the smallest amount.

= 7.7 ⋅ 17

= $130.9

After 15% fee,

= (1 - 0.15) ⋅ 130.9

= 0.85 ⋅ 130.9

= $111.265

Difference between the largest amount and the smallest amount :

= $268.345 - $111.265

= $157.08

≈ $157

Question 8 :

An engineer is designing a bridge of height h feet above the water. The bridge must include a ramp on either end. The ramps' bases must be at least 20 feet long for every 5 feet of bridge height. There is only room for 250 feet of ramp on one end of the bridge. If h is an integer, what is the largest possible value of h.

Answer :

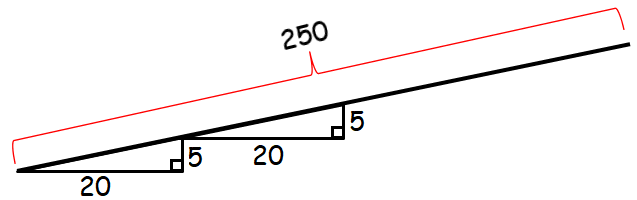
Using Pythagorean Theorem in one of the right triangles above,

(Hypotenuse)² = 20² + 5²

(Hypotenuse)² = 425

Hypotenuse ≈ 20.6155

For each 20.6155 feet length of the ramp, there is 5 feet height.

Number of parts of length 20.6155 each on the ramp of 250 feet length :

= ²⁵⁰⁄₂₀.₆₁₅₅

≈ 12.1268

Height of the bridge :

h = 5 ⋅ 12.1268

h = 60.634

h is an integer. The laregst possible value of h is 60.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.