SAT MATH GRAPHING SYSTEMS OF LINEAR INEQUALITIES

Solve each system of inequalities by graphing.

Example 1 :

x > -2

y ≤ 3

y > x - 1

Solution :

The corresponding equations are

x = -2

y = 3

y = x - 1

Use a dashed line for inequalities with < or > and a solid line for inequalities with ≤ or ≥.

Select (0, 0) as a test point for each inequality.

x > -2 ----> 0 > -2 (true)

y ≤ 3 ----> 0 ≤ 3 (true)

y > x - 1 ----> 0 > -1 (true)

The graph of the first inequality is the half plane right of the vertical line.

The graph of the second inequality is the half plane on and below the horizontal line.

The graph of the third inequality is the half plane above the line y = x - 1.

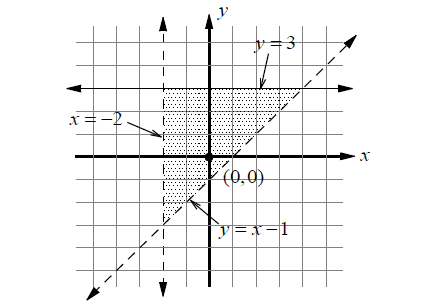
The graph of the system is the shaded region shown above.

Example 2 :

y ≤ 3x - 1

y > -2x

Solution :

The corresponding equations are

y = 3x - 1

y = -2x

Use a dashed line for inequalities with < or > and a solid line for inequalities with ≤ or ≥.

Select (0, 0) as a testing point for the first inequality.

y ≤ 3x - 1 ----> 0 ≤ -1 (false)

The point (0, 0) is not part of the solution. Shade the half plane on or below the line y = 3x - 1.

We cannot select (0, 0) as a test point for the second inequality y > -2x, because (0, 0) is on the boundary line.

We can use (0, 1) as a testing point.

y > -2x ----> 0 > -2 (true)

The point (0, 1) is part of the solution. Shade the half plane above the line y > -2x.

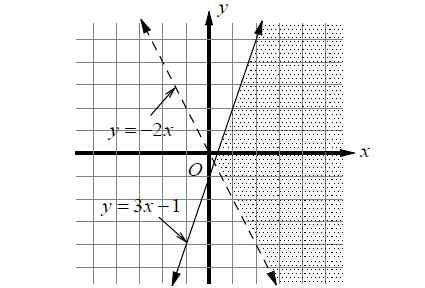
The graph of the system is the shaded region shown above.

Solved Problems

Problem 1 :

y - x ≥ 1

y ≤ -2x

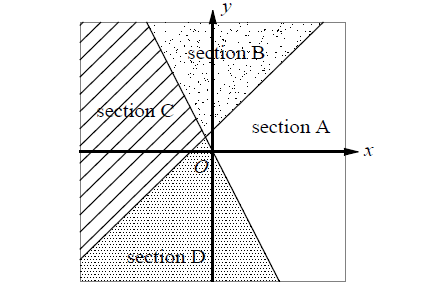
A system of inequalities and a graph are shown above. Which section or sections of the graph could represent all of the solutions to the system?

(A)  Section A

(B)  Section B

(C)  Section C

(D)  Section D

Solution :

y - x ≥ 1

y ≤ -2x

Select a point from each section, then test them on the inequalities. Let’s use (3, 0), (0, 3), (-3, 0) and (0, -3) from each section as test points.

(3, 0) from section A :

y - x ≥ 1 ----> -3 ≥ 1 (false)

y ≤ -2x ----> 0 ≤ -6 (false)

(0, 3) from section B :

y - x ≥ 1 ----> 3 ≥ 1 (true)

y ≤ -2x ----> 3 ≤ 0 (false)

(-3, 0) from section C :

y - x ≥ 1 ----> 3 ≥ 1 (true)

y ≤ -2x ----> -3 ≤ 0 (true)

(0, -3) from section D :

y - x ≥ 1 ----> -3 ≥ 1 (false)

y ≤ -2x ----> -3 ≤ 0 (true)

Since x = -3 and y = 0 are true for both inequalities, section C represents all of the solutions to the system.

Therefore, the correct answer is option (C).

Problem 2 :

Which of the following ordered pairs (x, y) is a solution to the system of inequalities

y > x - 4

x + y < 5

(A)  (4, -2)

(B)  (0, 2)

(C)  (5, 3)

(D)  (0, -5)

Solution :

y > x - 4

x + y < 5

Check each answer choice, to determine which ordered pair (x, y) is a solution to the system of inequalities.

(A)  (4, -2) :

y > x - 4 ----> -2 > 0 (false)

x + y < 5 ----> 2 < 5 (true)

(B)  (0, 2) :

y > x - 4 ----> 2 > -4 (true)

x + y < 5 ----> 2 < 5 (true)

(C)  (5, 3) :

y > x - 4 ----> 3 > 1 (true)

x + y < 5 ----> 8 < 5 (false)

(D)  (0, -5) :

y > x - 4 ----> -5 > -4 (false)

x + y < 5 ----> -5 < 5 (true)

(0, 2) is a solution to the system of inequalities because the ordered pair gives a true statement for both pairs of inequalities.

Therefore, the correct answer is option (B).

Problem 3 :

x - 2y ≤ -2

y < -x + 2

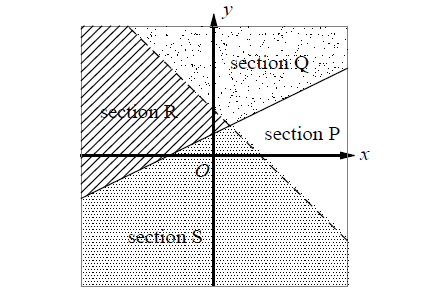
A system of inequalities and a graph are shown above. Which section or sections of the graph could represent all of the solutions to the system?

(A)  Section P

(B)  Section Q

(C)  Section R

(D)  Section S

Solution :

x - 2y ≤ -2

y < -x + 2

Select a point from each section, then test them on the inequalities. Let’s use (5, 0), (0, 5), (-5, 0) and (0, -5) from each section as test points.

(5, 0) from section P :

x - 2y ≤ -2 ----> 5 ≤ -2 (false)

y < -x + 2 ----> 0 ≤ -3 (false)

(0, 5) from section Q :

x - 2y ≤ -2 ----> -10 ≤ -2 (true)

y < -x + 2 ----> 5 < 2 (false)

(-5, 0) from section R :

x - 2y ≤ -2 ----> -5 ≤ -2 (true)

y < -x + 2 ----> 0 < 7 (true)

(0, -5) from section S :

x - 2y ≤ -2 ----> 10 ≤ 1 (false)

y < -x + 2 ----> -5 < 2 (true)

Since x = -5 and y = 0 are true for both inequalities, section R represents all of the solutions to the system.

Therefore, the correct answer is option (C).

Problem 4 :

2 - y < 2x

-x ≤ 4 - y

If the above system of inequalities is graphed on the xy-plane above. which quadrant contains no solutions to the system?

(A) Quadrant II

(B) Quadrant III

(C) Quadrant IV

(D) There are solutions in all four quadrants.

Solution :

Graph the given system of inequalities on the xy-plane.

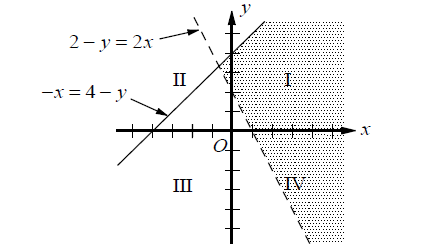
The solution to the system of inequalities is the shaded region as shown in the graph above. It can be seen that the solutions only include points in quadrants I, II and IV and do not include any points in quadrant III.

Therefore, the correct answer is option (B).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.