SAT MATH - ABSOLUTE VALUE EQUATIONS

The absolute value of a number is the distance on a number line between the graph of the number and the origin.

The distance between -3 and the origin is 3. Thus,

|-3| = 3

The distance between 3 and the origin is 3. Thus,

|3| = 3

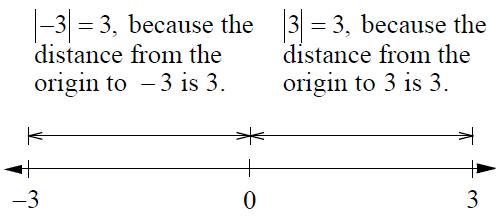
Therefore, if |x| = 3, then x = 3 or x = -3.

An absolute value function can be written using two or more expressions such as

How to Solve Absolute Value Equations

To solve any absolute value function, it has to be in the form of

|x + a| = k

Here, a and k are real numbers. And there should be only absolute part on the left side.

Let us consider the absolute value equation given below.

|2x + 3| = 5

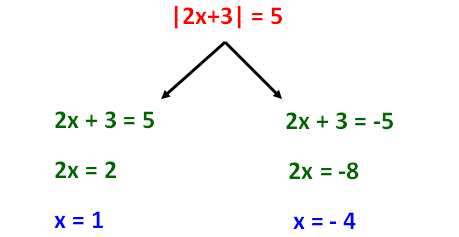
The following steps will be useful to solve absolute value equations.

Step 1 :

Get rid of absolute sign and split up into two branches.

Step 2 :

For the first branch, take the sign as it is on the right side.

Step 3 :

For the second branch, change the sign on the right side.

Step 4 :

Then solve both the branches.

How to Graph Absolute Value Functions

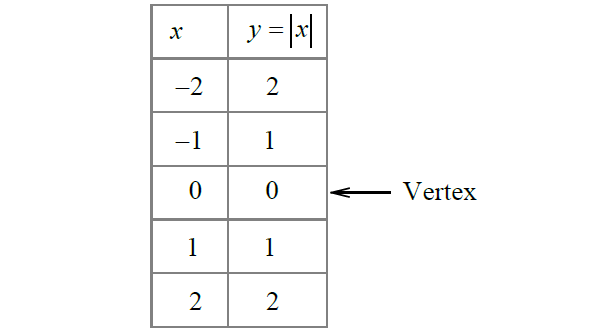
To sketch the graph of y = a|x + h| + k, use the following steps.

1. Find the x-coordinate of the vertex by finding the value of x for which x + h = 0.

2. Make a table of values using the -xcoordinate of the vertex. Find two -xvalues to its left and two to its right.

3. Plot the points from inside the table. If a > 0, the vertex will be the minimum point and if a < 0, the vertex will be the maximum point.

Table of values :

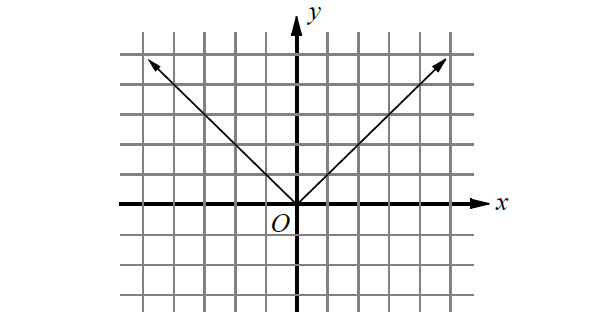
The graph of y = |x|.

Solved Problems

Problems 1-3 : Solve the absolute value equation.

Problem 1 :

|3x - 5| = 7

Solution :

3x - 5 = 7  or  3x - 5 = -7

3x = 12  or  3x = -2

x = 4  or  x = -⅔

Problem 2 :

|x + 5| = 0

Solution :

|x + 5| = 0

x + 5 = 0

x = -5

Problem 3 :

|x - 2| = -5

Solution :

|x - 2| = -5 means that the distance between x and 2 is -5. Since distance cannot be negative, the given absolute value equation has no solution.

Problem 4 :

Which of the following expressions is equal to -1 for some values of x?

(A)  |1 - x| + 6

(B)  |1 - x| + 4

(C)  |1 - x| + 2

(D)  |1 - x| - 2

Solution :

By definition, the absolute value of any expression is a nonnegative number. 

In options (A), (B) and (C),

|1 - x| + 6 > 0

|1 - x| + 4 > 0

|1 - x| + 2 > 0

So, the expressions in options (A), (B) and (C) can not be equal to -1.

In option (D), |1 - x| - 2 could be a negative value.

|1 - x| - 2 = -1

|1 - x| = 1

1 - x = 1  or  1 - x = -1

-x = 0  or  -x = -2

x = 0  or  x = 2

Therefore, the correct answer is option (D).

Problem 5 :

If |2x + 7|= 5, which of the following could be the value of x?

(A)  -6

(B)  -4

(C)  -2

(D)  0

Solution :

|2x + 7|= 5

2x + 7 = 5  or  2x + 7 = -5

2x = -2  or  2x = -12

x = -1  or  x = -6

Therefore, the correct answer is option (A).

Problem 6 :

For what value of x is |x - 1| - 1 equal to 1?

(A)  -1

(B)  0

(C)  1

(D)  2

Solution :

|x - 1| - 1 = 1

x - 1 = 1  or  x - 1 = -1

x = 2  or  x = 0

Therefore, the correct answer is option (B).

Problem 7 :

For what value of x is |3x - 5| equal to -1?

(A)  -2

(B)  -1

(C)  0

(D)  There is no such value of x.

Solution :

Given :

|3x - 5| = -1

Absolute value of any expression can never be negative. So, the equation |3x - 5| = -1 has no solution.

Therefore, the correct answer is option (D).

Problem 8 :

For what value of x is 2|x + 5| - 8 equal to 0?

Solution :

2|x + 5| - 8 = 0

2|x + 5| = 8

|x + 5| = 4

x + 5 = 4  or  x + 5 = -4

x = -1  or  x = -9

Problem 9 :

For what value of x is 3 - |3 - x| equal to 3?

Solution :

3 - |3 - x| = 3

-|3 - x| = 0

|3 - x| = 0

3 - x = 0

x = 3

Problem 10 :

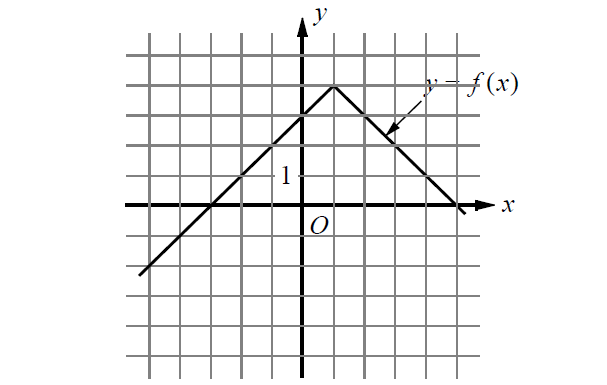
The graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its maximum?

(A)  -3

(B)  -1

(C)  1

(D)  3.

Solution :

The maximum value of the function corresponds to the y- coordinate of the point on the graph, which is highest along the vertical axis. The highest point along the y- axis has coordinates (1, 4). 

When f(x) is maximum, the value of x is 1.

Therefore, the correct answer is option (C).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.