ROTATIONS AND ROTATIONAL SYMMETRY

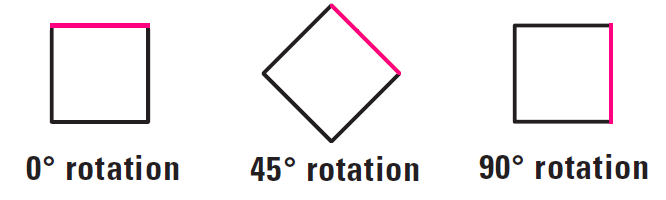
A figure in the plane has rotational symmetry, if the figure can be mapped onto itself by rotation of 180° or less.

For instance, a square has rotational symmetry because it maps onto itself by a rotation of 90°.

Rotations in a Coordinate Plane

Example 1 :

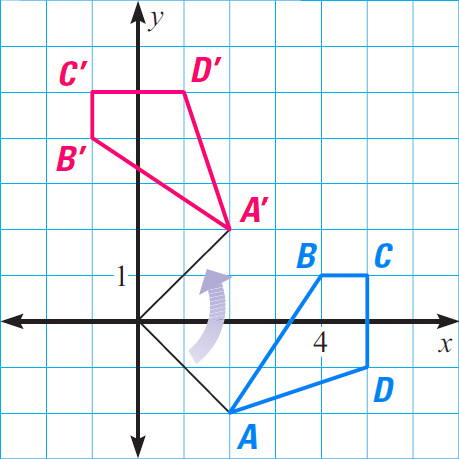
In a coordinate plane, sketch the quadrilateral whose vertices are A(2, - 2), B(4, 1), C(5, 1), and D(5, - 1). Then, rotate ABCD 90° counterclockwise about the origin and name the coordinates of the new vertices. Describe any patterns you see in the coordinates.

Solution :

Plot the points, as shown in blue. Use a protractor, a compass, and a straightedge to find the rotated vertices. The coordinates of the preimage and image are listed below.

In the list above, the x-coordinate of the image is the opposite of the y-coordinate of the preimage. The y-coordinate of the image is the x-coordinate of the preimage.

This transformation can be described as

(x, y) ----> (-y, x)

Identifying Rotational Symmetry

Example 2 :

Does the figure shown below have rotational symmetry?

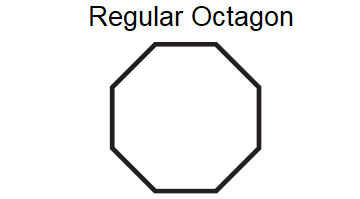
Solution :

The regular octagon shown above has rotational symmetry. It can be mapped onto itself by a clockwise or counterclockwise rotation of 45°, 90°, 135° or 180° about its center.

Example 3 :

Does the figure shown below have rotational symmetry?

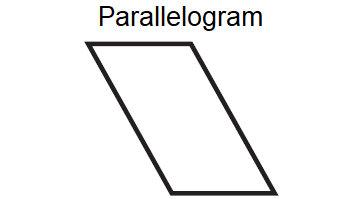
Solution :

The parallelogram regular shown above has rotational symmetry. It can be mapped onto itself by a clockwise or counterclockwise rotation of 180° about its center.

Example 4 :

Does the figure shown below have rotational symmetry?

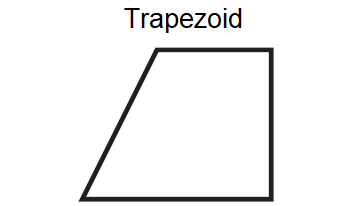
Solution :

The trapezoid shown above does not have rotational symmetry.

Using Rotational Symmetry

Example 5 :

A music store called Ozone is running a contest for a store logo. The winning logo will be displayed on signs throughout the store and in the store’s advertisements. The only requirement is that the logo include the store’s name. Two of the entries are shown below. What do you notice about them?

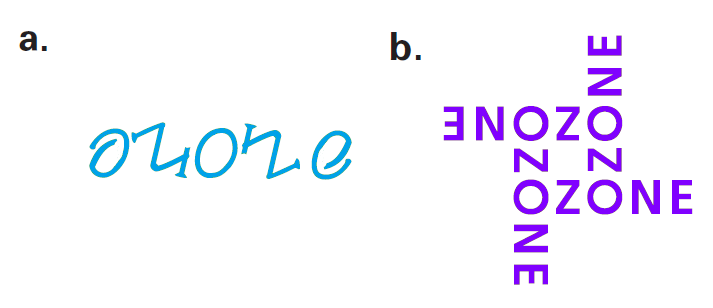
Solution (a) :

This design has rotational symmetry about its center. It can be mapped onto itself by a clockwise or counterclockwise rotation of 180°.

Solution (b) :

This design also has rotational symmetry about its center. It can be mapped onto itself by a clockwise or counterclockwise rotation of 90° or 180°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.