ROTATION OF 90 DEGREES ABOUT THE ORIGIN

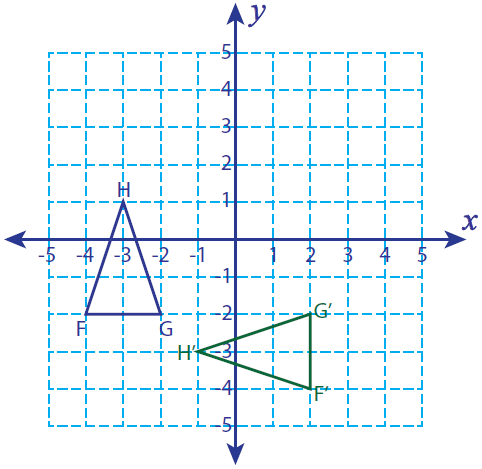
Problem 1 :

Let F(-4, -2), G(-2, -2) and H(-3, 1) be the three vertices of a triangle. If this triangle is rotated 90° counterclockwise, find the vertices of the rotated figure and graph.

Solution :

Step 1 :

Here, triangle is rotated 90° counterclockwise. So the rule that we have to apply here is

(x, y) ----> (-y, x)

Step 2 :

Based on the rule given in step 1, we have to find the vertices of the rotated figure.

Step 3 :

(x , y) ----> (-y , x)

F(-4 , -2) ----> F'(2, -4)

G(-2, -2) ----> G'(2, -2)

H (-3, 1) ----> H'(-1, -3)

Step 4 :

Vertices of the rotated figure are

F'(2, -4), G'(2, -2) and H'(-1, -3)

Problem 2 :

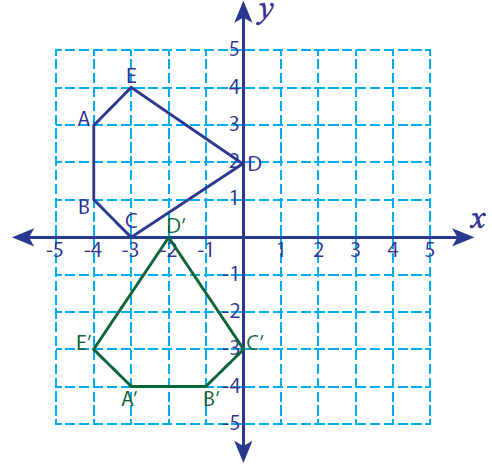
Let A(-4, 3), B(-4, 1), C(-3, 0), D(0, 2) and E(-3,4) be the vertices of a closed figure. If this figure is rotated 90° counterclockwise, find the vertices of the rotated figure and graph.

Solution :

Step 1 :

Here, triangle is rotated 90° counterclockwise. So the rule that we have to apply here is

(x, y) ----> (-y, x)

Step 2 :

Based on the rule given in step 1, we have to find the vertices of the rotated figure.

Step 3 :

(x, y) ----> (-y, x)

A(-4, 3) ----> A'( -3, -4)

B(-4, 1) ----> B'(-1, -4)

C(-3, 0) ----> C'(0, -3)

D(0, 2) ----> D'(-2, 0)

E(-3, 4) ----> E'(-4, -3)

Step 4 :

Vertices of the rotated figure are

A'(-3, -4), B'(-1, -4), C'(0, -3), D'(-2, 0) and E'(-4, -3)

Problem 3 :

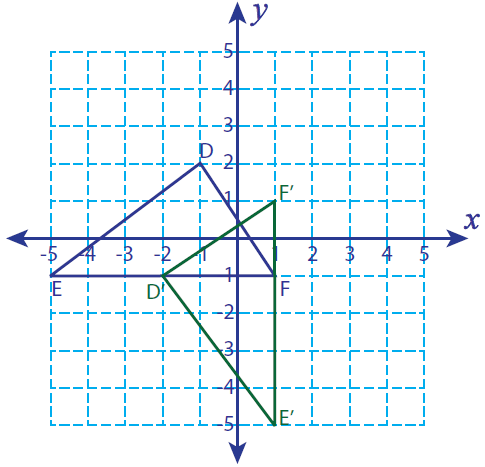
Let D(-1, 2), E(-5, -1) and F(1, -1) be the vertices of a triangle. If the triangle is rotated 90° counterclockwise, find the vertices of the rotated figure and graph.

Solution :

Step 1 :

Here, triangle is rotated 90° counterclockwise. So the rule that we have to apply here is

(x, y) ----> (-y, x)

Step 2 :

Based on the rule given in step 1, we have to find the vertices of the rotated figure.

Step 3 :

(x, y) ----> (-y, x)

D(-1, 2) ----> D'(-2, -1)

E(-5, -1) ----> E'(1, -5)

F(1, -1) ----> F'(1, 1)

Step 4 :

Vertices of the rotated figure are

D'(-2, -1) , E'(1, -5) and F'(1, 1)

Problem 4 :

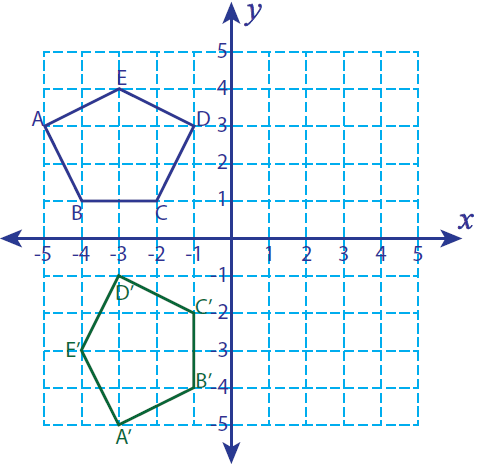
Let A(-5, 3), B(-4, 1), C(-2, 1) D(-1, 3) and E(-3,  4) be the vertices of a closed figure. If this figure is rotated 90° counterclockwise, find the vertices of the rotated figure and graph.

Solution :

Step 1 :

Here, triangle is rotated 90° counterclockwise. So the rule that we have to apply here is

(x, y) ----> (-y, x)

Step 2 :

Based on the rule given in step 1, we have to find the vertices of the rotated figure.

Step 3 :

(x, y) ----> (-y, x)

A(-5, 3) ----> A'(-3, -5)

B(-4, 1) ----> B'(-1, -4)

C(-2, 1) ----> C'(-1, -2)

D(-1, 3) ----> D'(-3, -1)

E(-3, 4) ----> E'(-4, -3)

Step 4 :

Vertices of the rotated figure are

A'(-3, -5), B'(-1, -4), C'(-1, -2), D'(-3, -1) and E'(-4, -3)

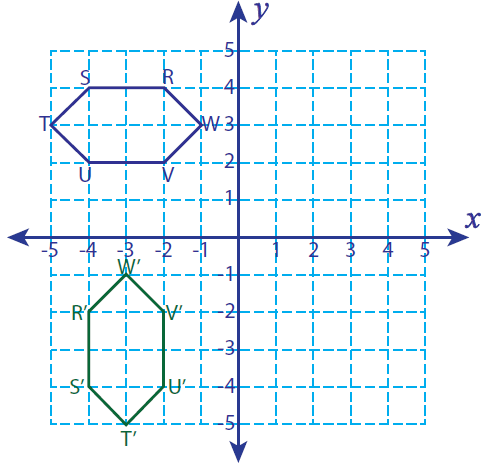
Problem 5 :

Let R(-2, 4), S(-4, 4), T(-5, 3) U(-4, 2) and V(-2, 2) be the vertices of a closed figure. If this figure is rotated 90° counterclockwise, find the vertices of the rotated figure and graph.

Solution :

Step 1 :

Here, triangle is rotated 90° counterclockwise. So the rule that we have to apply here is

(x, y) ----> (-y, x)

Step 2 :

Based on the rule given in step 1, we have to find the vertices of the rotated figure

Step 3 :

(x, y) ----> (-y, x)

R(-2, 4) ----> R'(-4, -2)

S(-4, 4) ----> S'(-4, -4)

T(-5, 3) ----> T'(-3, -5)

U(-4, 2) ----> U'(-2, -4)

V(-2, 2) ----> V'(-2, -2)

Step 4 :

Vertices of the rotated figure are

R'(-4, -2), S'(-4, -4), T'(-3, -5), U'(-2, -4) and E'(-2, -2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.