ROOTS OF CUBIC EQUATION

Example 1 :

Solve the following cubic equation whose roots are in arithmetic progression. 

x³ - 12x² + 39 x - 28 = 0

Solution :

When we solve cubic equation we will get three roots. 

Since the roots are in arithmetic progression, the roots can be taken as given below.

p - q, p, p + q

Compare :

x³ - 12x² + 39x - 28 = 0 and ax³ + bx² + cx + d = 0

a = 1, b = -12, c = 39, d = -28

Sum of the roots = -b/a

p - q + p + p + q = -(-12)/1

3p = 12

p = 4

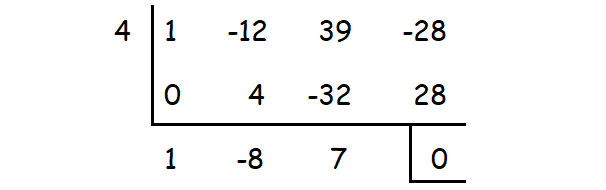
4 is one of the roots. The other roots can be determined by solving the quadratic equation

x² - 8x + 7 = 0

x² - 8x + 7 = 0

(x - 1)(x - 7) = 0

x - 1 = 0 or x - 7 = 0

x = 1 or x = 7

Therefore the roots are 1, 4 and 7.

Example 2 :

Solve the following cubic equation whose roots are in geometric progression. 

x³ - 19x² + 114x - 216 = 0

Solution :

When we solve cubic equation we will get three roots. 

Since the roots are in geometric progression, the roots can be taken as given below.

p/q, p, pq

Compare :

x³ - 19x² + 114x - 216 = 0 and ax³ + bx² + cx + d = 0

a = 1, b = -19, c = 114, d = -216

Product of roots = -d/a

p/q ⋅ p ⋅ pq = -(-216)/1

p³ = 216

p³ = 6³

p = 6

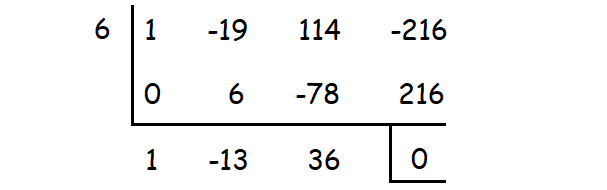
6 is one of the roots. The other roots can be determined by solving the quadratic equation

x² - 13x + 36 = 0

(x - 4)(x - 9) = 0

x - 4 = 0 or x - 9 = 0

x = 4 or x = 9

Therefore the roots are 4, 6 and 9.

Example 3 :

Solve for x : 2x³ – 3x² – 8x – 3 = 0

Solution :

Let p(x) = 2x³ – 3x² – 8x – 3

When x = -1

p(-1) = 2(-1)³ – 3(-1)² – 8(-1) – 3

= -2 - 3 + 8 - 3

= -8 + 8

= 0

So, -1 is one of the roots of the cubic equation.

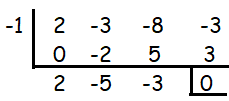
2x² - 5x - 3 = 0

2x² - 6x + 1x - 3 = 0

2x(x - 3) + 1(x - 3) = 0

(2x + 1)(x - 3) = 0

2x + 1 = 0 and x - 3 = 0

2x = -1 and x = 3

x = -1/2 and x = 3

So, the solutions are -1, -1/2 and 3.

Example 4 :

Solve for x : 2x³ – x² – x = 0

Solution :

Let p(x) = 2x³ – x² – x

Factoring x, we get

= x(2x² – x – 1)

Since p(x) = 0

x(2x² – x – 1) = 0

x = 0 and 2x² – x – 1 = 0

2x² – 2x + 1x – 1 = 0

2x(x - 1) + 1(x - 1) = 0

(2x + 1) (x - 1) = 0

2x + 1 = 0 and x - 1 = 0

2x = -1 and x = 1

x = -1/2 and x = 1

So, the solutions are x = -1/2, 0 and 1.

Example 5 :

Solve for x : x³ – x = 0

Solution :

Let p(x) = x³ – x = 0

Factoring x, we get

= x(x² – 1)

Since p(x) = 0

x(x² – 1) = 0

x = 0 and x² – 1 = 0

x² = 1

x = -1 and 1

So, the solutions are 0, -1 and 1.

Example 6 :

Solve for x : (2/3)x³ – 18 = 0

Solution :

Let p(x) = (2/3)x³ – 18 = 0 

(2/3)x³ = 18

x³ = 18 (3/2)

x³ = 9 (3)

x³ = 27

x³ = 3³

x = 3

So, the value of x is 3, we have repeating roots.

Example 7 :

The roots of the cubic equations x³ - 7x + 6 = 0 are

a)  1, 2 and 3     b)  1, -2 and 3

c)  1, 2 and -3     d)  1, -2 and -3

Solution :

Using synthetic division, let us check if the cubic polynomial has the root 1.

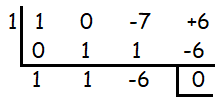
While dividing the polynomial by 1, we get 0 as remainder, then 1 is one of the roots of the polynomial.

x² + x - 6 = 0

x² + 3x - 2x - 6 = 0

x(x + 3) - 2(x + 3) = 0

(x - 2)(x + 3) = 0

x - 2 = 0 and x + 3 = 0

x = 2 and x = -3

So, the solutions are -3, 1 and 2.

Example 8 :

The roots of the cubic equations x³ + 9x² - x - 9 = 0 are

a)  1, 2 and 3     b)  1, -1 and -9

c)  1, 3 and -9     d)  1, 3 and 9

Solution :

Using the method of factoring, we get

x³ + 9x² - x - 9 = 0

x²(x + 9) - 1(x + 9) = 0

(x² - 1)(x + 9) = 0

x² - 1 = 0

x² = 1 and x + 9 = 0

x = -1, 1 and -9

So, the solutions are -1, 1 and -9, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.