RIGID MOTION IN A PLANE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Figures in a plane can be reflected, rotated or translated to produce new figures. The new figure is called the image and original figure is called the preimage.
The operation that maps, or moves, the preimage onto the image is called a transformation.
In this section, we will learn about three basic transformations - reflections, rotations and translations - and combinations of these. For each of three transformations below, the purple figure is the preimage and the green figure is the image.
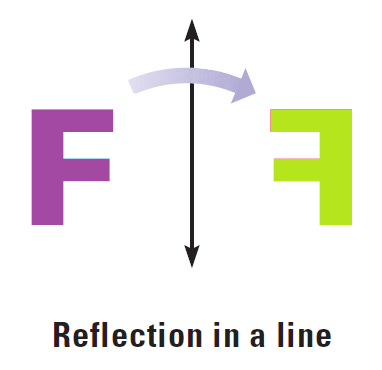
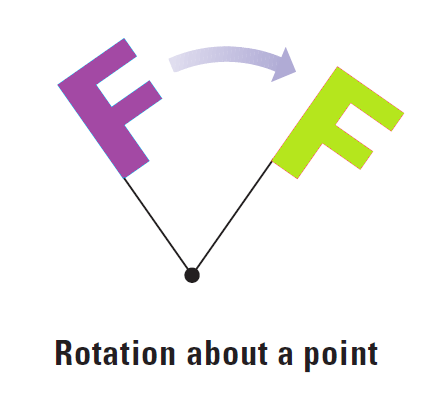
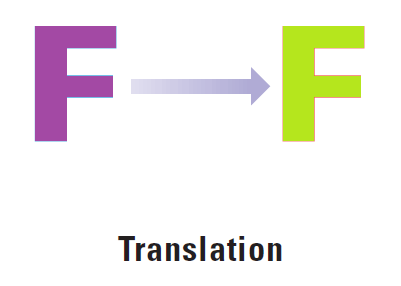
Naming Transformations
Example 1 :
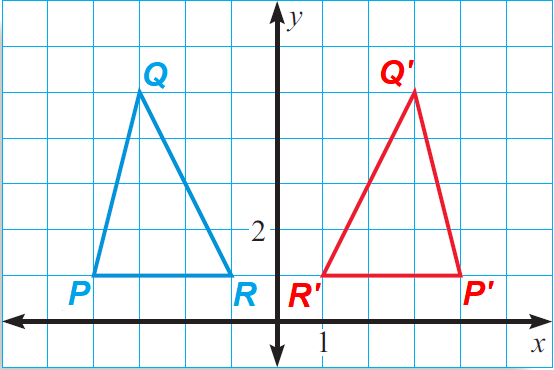
Use the graph of the transformation below.
a. Name and describe the transformation.
b. Name the coordinates of the vertices of the image.
c. Is triangle ABC congruent to image?
Solution (a) :
The transformation is a reflection in the y-axis. We can imagine that image has been obtained by flipping ΔPQR over the y-axis.
Solution (b) :
The coordinates of the vertices of the image, ΔP'Q'R' are P'(4, 1), Q'(3, 5) and R'(1, 1).
Solution (c) :
Yes, ΔPQR is congruent to its image ΔP'Q'R'. One way to show this would be to use the Distance Formula to find the lengths of the sides of both triangles. Then use the SSS congruence postulate.
Identifying Isometries
Example 2 :
Say, whether the following transformation appear to be isometry.
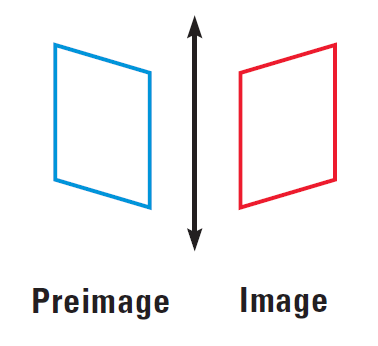
Solution :
This transformation appears to be an isometry. The blue parallelogram is reflected in a line to produce a congruent red parallelogram.
Example 3 :
Do you think that the following transformation appear to be isometry ? Explain your answer.
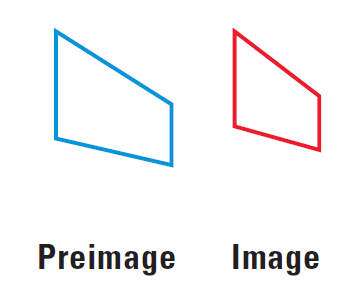
Solution :
No, this transformation is not an isometry. Because the image is not congruent to the preimage.
Example 4 :
Is the following transformation appear to be isometry?
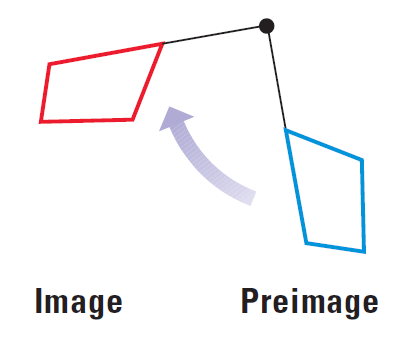
Solution :
Yes, this transformation appears to be an isometry. The blue quadrilateral is rotated about a point to produce a congruent a congruent red quadrilateral.
Mappings
Example 5 :
How can we describe the transformation shown below?
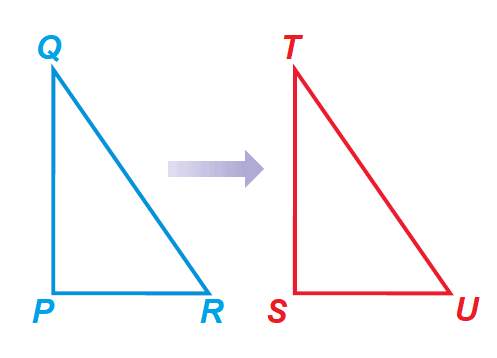
Solution :
We can describe the transformation shown above by writing,
"ΔPQR is mapped onto ΔSTU"
We can also use arrow notation as follows :
ΔPQR ----> ΔSTU
The order in which the vertices are listed specifies the correspondence. Either of the descriptions implies that
P ----> S
Q ----> T
R ----> U
Preserving Length and Angle Measure
Example 6 :
In the diagram shown below, ΔABC is mapped onto ΔXYZ. The mapping is a rotation. Given that ΔABC ---> ΔXYZ is an isometry, find the length of XY and the measure of ∠Z.
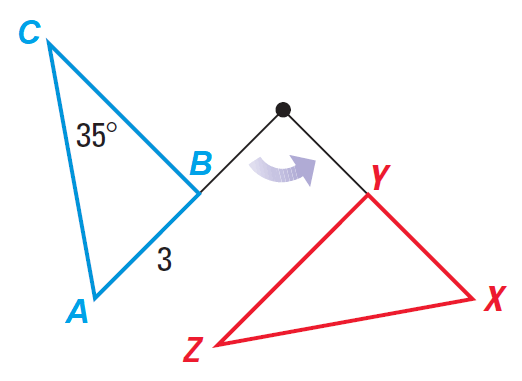
Solution :
The statement "ΔABC is mapped onto ΔXYZ" implies that,
A ----> X
B ----> Y
C ----> Z
Because the transformation is an isometry, the two triangles are congruent.
So, we have
AB = XY = 3 units
∠R = ∠Z = 35°
Identifying Transformations
Example 7 :
We are assembling pieces of wood to complete a railing for our porch. The finished railing should resemble the one below.

a. How are pieces 1 and 2 related ? pieces 3 and 4?
b. In order to assemble the rail as shown, explain why we need to know how the pieces are related.
Solution (a) :
Pieces 1 and 2 are related by a rotation. Pieces 3 and 4 are related by a reflection.
Solution (b) :
Knowing how the pieces are related helps us manipulate the pieces to create the desired pattern.
Using Transformations in Real Life
Example 8 :
Many building plans for kayaks show the layout and dimensions for only half of the kayak. A plan of the top view of a kayak is shown below.

a. What type of transformation can a builder use to visualize plans for the entire body of the kayak?
b. Using the plan above, what is the maximum width of the entire kayak?
Solution (a) :
The builder can use a reflection to visualize the entire kayak. For instance, when one half of the kayak is reflected in a line through its center, you obtain the other half of the kayak.
Solution (b) :
The two halves of the finished kayak are congruent, so the width of the entire kayak will be 2(10), or 20 inches.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

