RHOMBUSES RECTANGLES AND SQUARES

In this section, we will study study three special types of parallelograms : rhombuses, rectangles and squares.

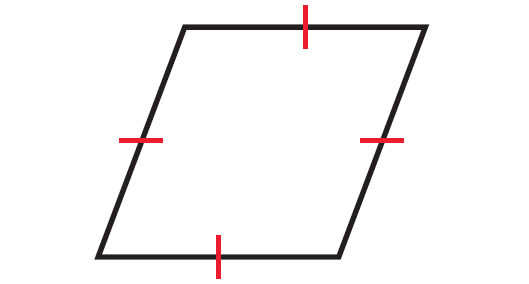
Rhombus :

A rhombus is a parallelogram with four congruent sides.

Rectangle :

A rectangle is a parallelogram with four right angles.

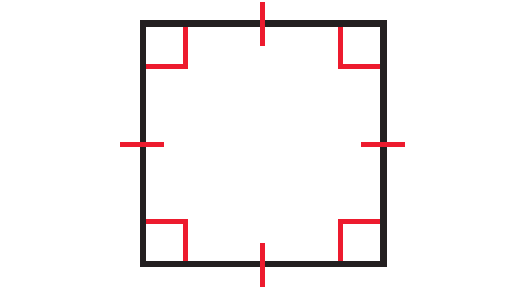
Square :

A square is a parallelogram with four congruent sides and four right angles.

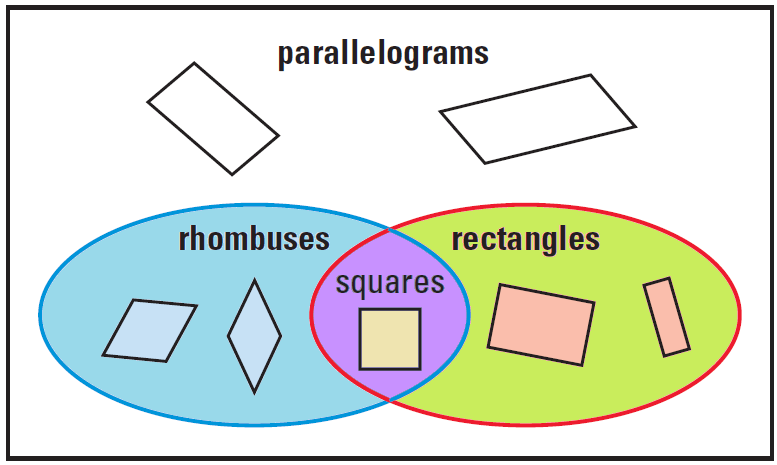
The Venn diagram given below shows the relationships among parallelograms, rhombuses, rectangles and squares. Each shape has the properties of every group that it belongs to.

For instance, a square is a rectangle, a rhombus, and a parallelogram, so it has all of the properties of each of those shapes.

Corollaries about Special Quadrilaterals

Rhombus Corollary :

A quadrilateral is a rhombus, if and only if it has four congruent sides.

Rectangle Corollary :

A quadrilateral is a rectangle, if and only if it has four right angles.

Square Corollary :

A quadrilateral is a square, if and only if it is a rhombus and a rectangle.

Theorems

Theorem 1 :

A parallelogram is a rhombus, if and only if its diagonals are perpendicular.

It has been illustrated in the diagram shown below.

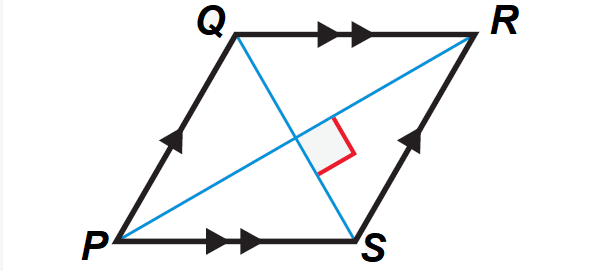
In the diagram above, ABCD is a rhombus if and only if

PR ⊥ QS

Theorem 2 :

A parallelogram is a rhombus, if and only if each diagonal bisects a pair of opposite angles.

It has been illustrated in the diagram shown below.

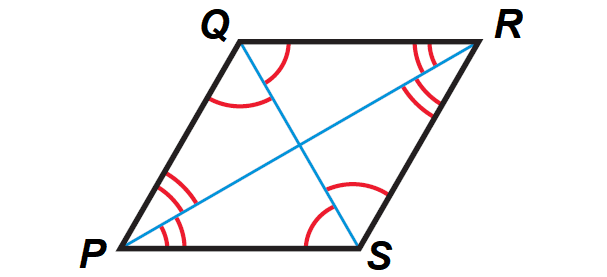
In the diagram above, PQRS is a rhombus if and only if

PR bisects ∠SPQ and ∠QRS

and

QS bisects ∠PSR and ∠PQR

Theorem 3 :

A parallelogram is a rectangle, if and only if its diagonals are congruent.

It has been illustrated in the diagram shown below.

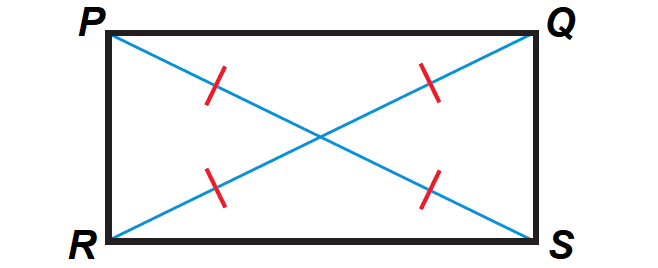
In the diagram above, PQRS is a rectangle if and only if

PS ≅ QR

Solved Questions

Question 1 :

Decide whether the statement given below is always, sometimes or never true.

"A rhombus is a rectangle"

Answer :

The statement is sometimes true.

In the Venn diagram above, the regions for rhombuses and rectangles overlap. If the rhombus is a square, it is a rectangle.

Question 2 :

Decide whether the statement given below is always, sometimes or never true.

"A parallelogram is a rectangle"

Answer :

The statement is sometimes true. Some parallelograms are rectangles.

In the Venn diagram above, we can see that some of the shapes in the parallelogram box are in the region for rectangles, but many aren’t.

Question 3 :

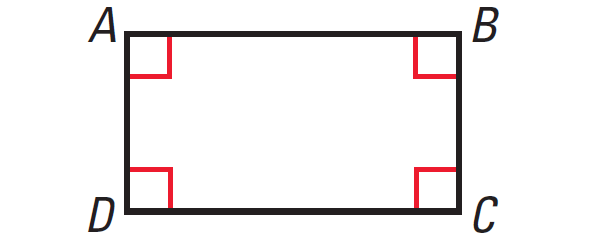
ABCD is a rectangle. What else do you know about ABCD?

Answer :

Because ABCD is a rectangle, it has four right angles by the definition. The definition also states that rectangles are parallelograms.

So, ABCD has all the properties of a parallelogram :

• Opposite sides are parallel and congruent.

• Opposite angles are congruent and consecutive angles are supplementary.

• Diagonals bisect each other.

Question 4 :

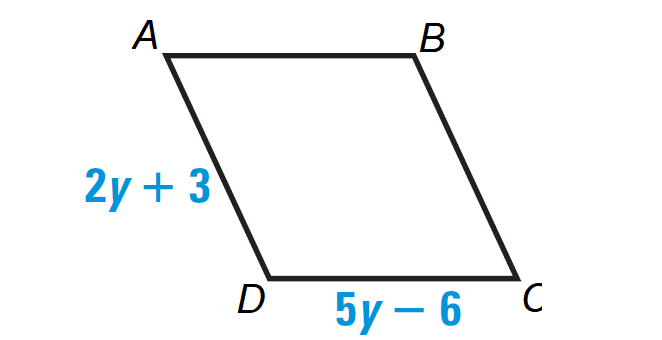
In the diagram at the right, PQRS is a rhombus. What is the value of y?

Answer :

All four sides of a rhombus are congruent, so we have

RS = PS

Substitute RS = 5y - 6 and PS = 2y + 3.

5y - 6 = 2y + 3

Add 6 to both sides.

5y = 2y + 9

Subtract 2y from

3y = 9

Divide both sides by 3.

y = 3

Question 5 :

Prove that the diagonals of a rhombus are perpendicular.

Answer :

Let us consider the rhombus PQRS as shown below.

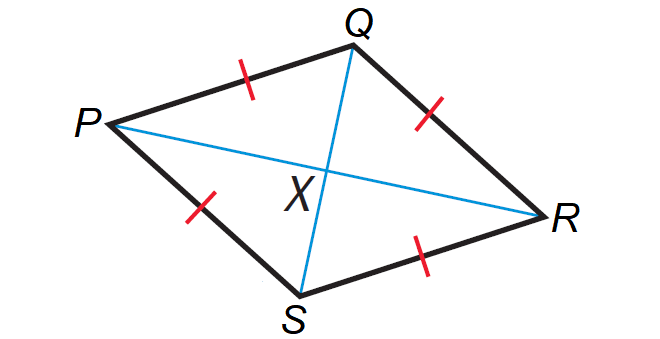
In the rhombus PQRS above, we have to prove

PR ⊥ QS

PQRS is a rhombus, so we have

PQ ≅ QR

Because the rhombus PQRS is also a parallelogram, its diagonals bisect each other.

So, we have

PX ≅ RX

PQ ≅ QR

Using SSS postulate, we have

ΔPXQ ≅ ΔRXQ

So, we have

∠PXQ ≅ ∠RXQ ----> ∠PXQ = ∠RXQ

Because ∠PXQ, ∠RXQ form a linear pair and ∠PXQ = ∠RXQ, we have

∠PXQ = ∠RXQ = 90°

Hence, we have

PR ⊥ QS

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.